Home
Class 11
PHYSICS
The sphere at P is given a downward velo...

The sphere at `P` is given a downward velocity `v_(0)` and swings in a vertical plane at the end of a rope of `l=1m` attached to a support at `O`. The rope breaks at angle `30^(@)` from horizontal , knowing that it can withstand a maximum tension equal to three times the weight of the sphere. Then the value of `v_(0)` will be `:`
`(g=pi ^(2) m//s^(2))`

A

`(g)/(2) m//s`

B

`(2g)/(3)m//s`

C

`sqrt((3g)/(2))m//s`

D

will have minimum value `(3)/(8)m`

Text Solution

Verified by Experts

The correct Answer is:
C
`T=mg sin theta=(mv^(2))/(R)`
`rArr 3mg-mg sin 30^(@)`
`=(m.(u_(0)^(2)+2glsin 30^(@)))/(l)`
`:. u_(0)=sqrt(3g//2)`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 82|4 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 83|6 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 80|4 Videos

  • CURRENT ELECTRICITY

    RESONANCE|Exercise Exercise|54 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

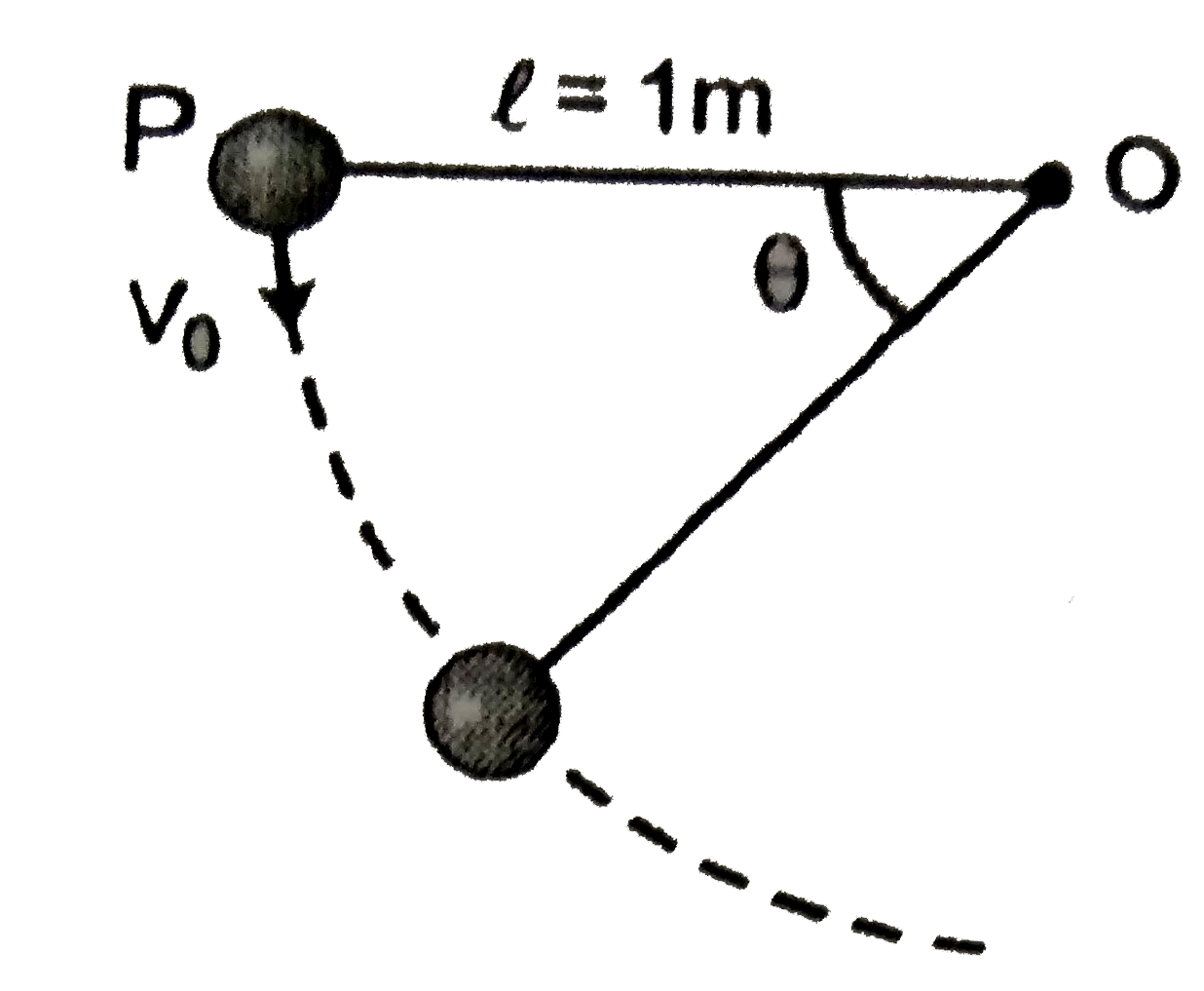
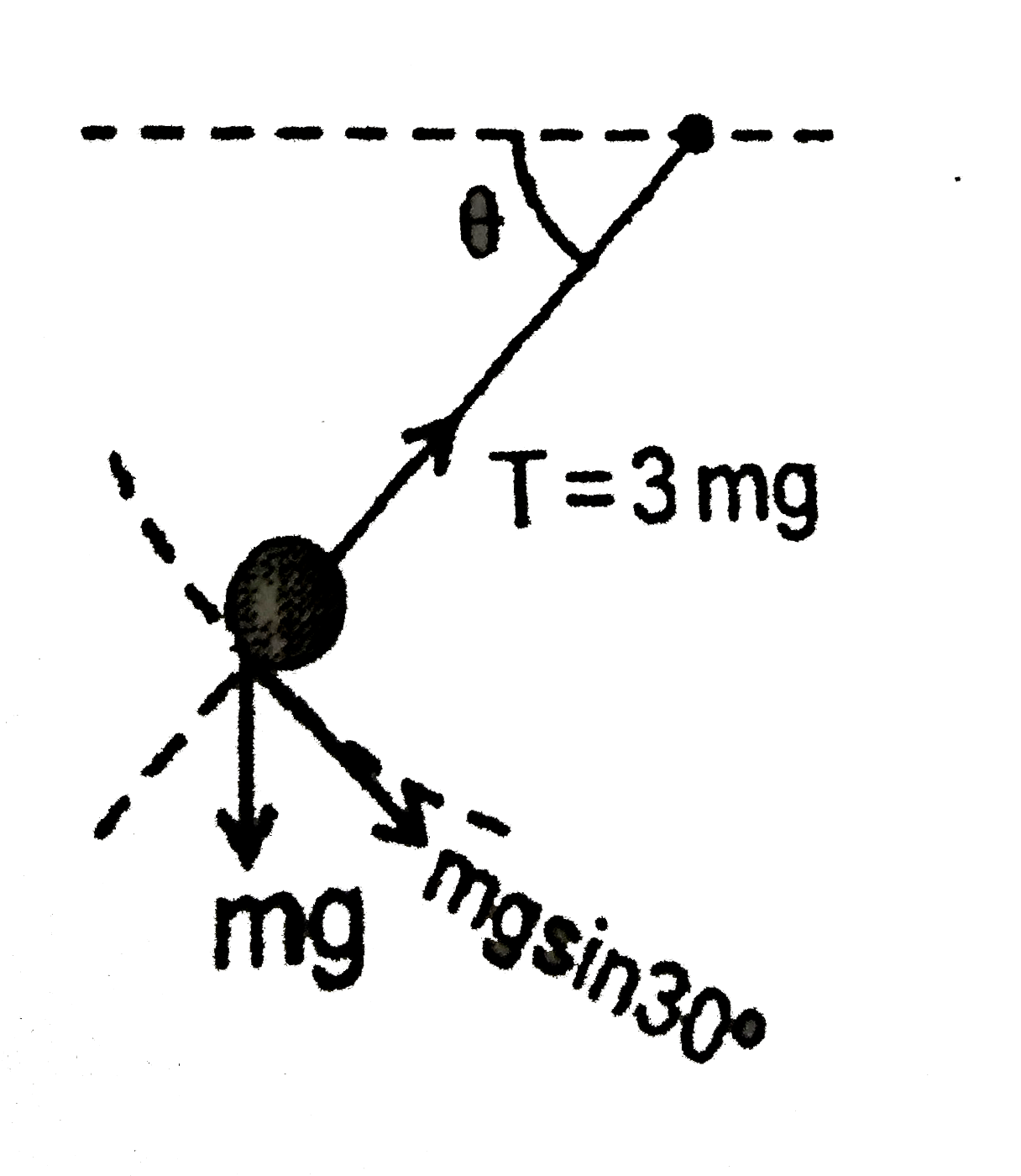
The sphere at P is given a down ward velocity v_(0) and swings in a vertical plane at the end of a rope of l = 1m attached to a support at O . The rope breaks at angle 30^@ from horizontal, knowing that it can withstand a maximum tension equal to four times the weight of the sphere. then the value of v_(0) will be (g = 10 m//s^(2)) . .

The sphere at A is given a downward velocity v_(0) of magnitude 5m//s and swings in a vertical plane at the end of a rope of length l=2m attached to a support at O . Determine the angle theta at which the rope will breack, knowing that it can withstant a maximum tension equal to twich the weight of the sphere.

A small sphere is given vertical velocity of magnitude v_0=5ms^-1 and it swings in a vertical plane about the end of a massless string. The angle theta with the vertical at which string will break, knowing that it can withstand a maximum tension equal to twice the weight of the sphere, is

A monkey of mass 30 kg climbs a rope which can withstand a maximum tension of 360 N. The maximum acceleration which this rope can tolerate for the climbing of monkey is: (g=10m//s^(2))

A particle of mass 1 kg is projected at an angle of 30^(@) with horizontal with velocity v = 40 m/s . The change in linear momentum of the particle after time t = 1 s will be (g = 10 m// s^(2) )

A body of mass 40 kg wants to climb up a rope hanging vertically. The rope can withstands a maximum tension of 500 N. What is the maximum acceleration with which the boy can climb rope? Tak e g=10m//s^(2)

A monkey of mass 40 kg climbs on a massless rope which can stand a maximum tension of 500 N. In which of the following cases will the rope break? ("Take g"=10m s^(-2))

A bob tied to the end of a string of length 2m, other end of which is fixed at a point in a vertical wall at a point O. The bob is imparted a vertical downward velocity of 5 m//s when the string is horizontal and swings in a vertical plane. Find the angular displacement of the bob from its initial position, when the string breaks. Given that the tensile strength of the string is twice the weight of the bob. Take g=10 m//s^(2)