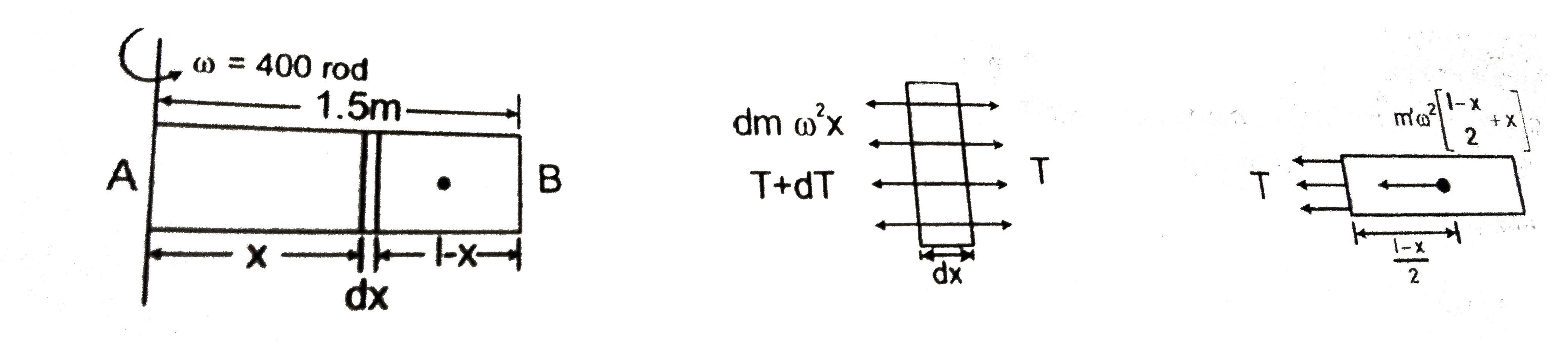Text Solution
Verified by Experts
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 90 Illustration|2 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 91 illustration|2 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise Now answer the following :|20 VideosCURRENT ELECTRICITY
RESONANCE|Exercise Exercise|54 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEMS-dpp 89 illustration
- One end of a wire 2m long and 0.2 cm^2 in cross section is fixed in a ...
Text Solution
|
- Find out longitudinal stress and tangential stress on a fixed block.
Text Solution
|
- Two blocks of masses 1 kg and 2kg are connect by a metal wire going ov...
Text Solution
|
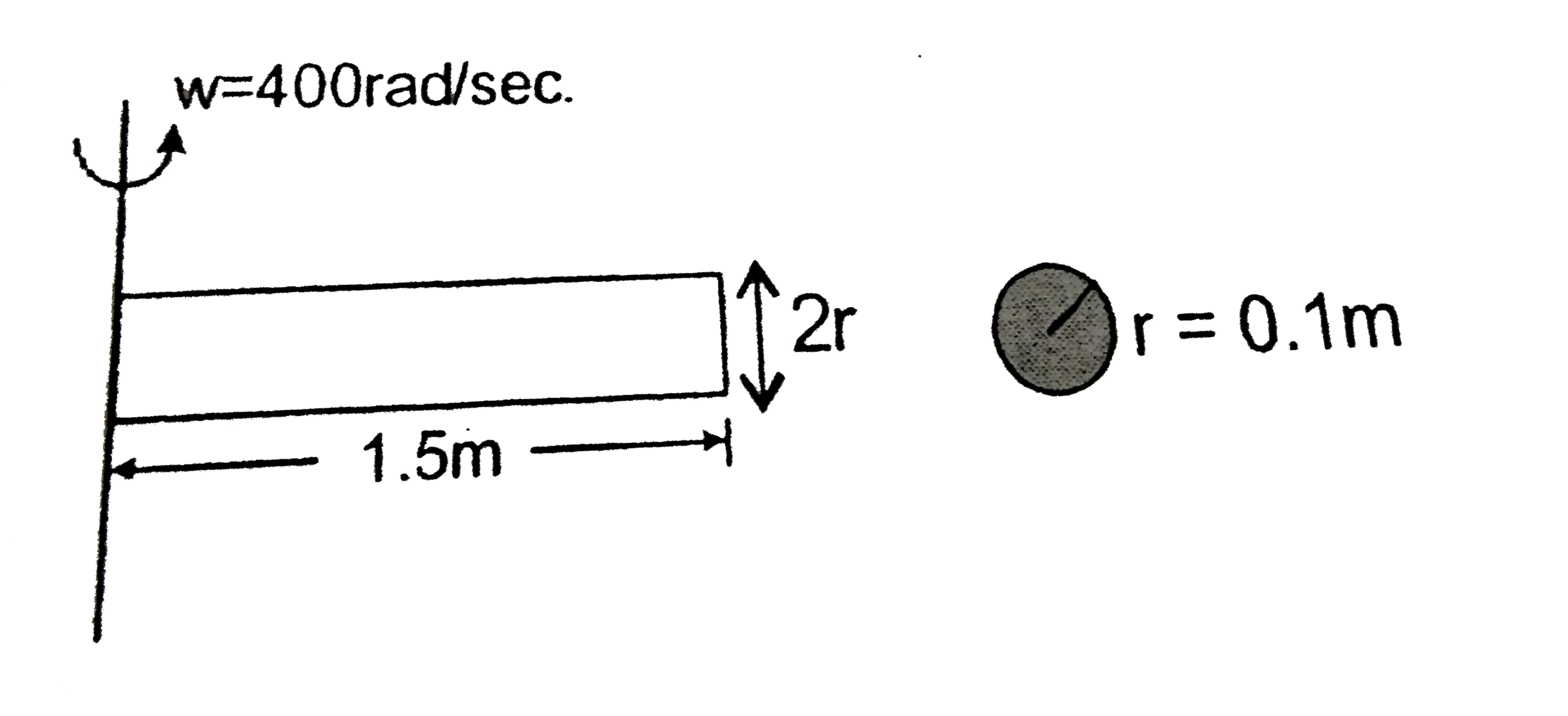
- A rod of 1.5m length and uniform density 10^(4)kg//m^(3) is rotating a...
Text Solution
|
- Find out the elongation in block. If mass area of cross-section and yo...
Text Solution
|