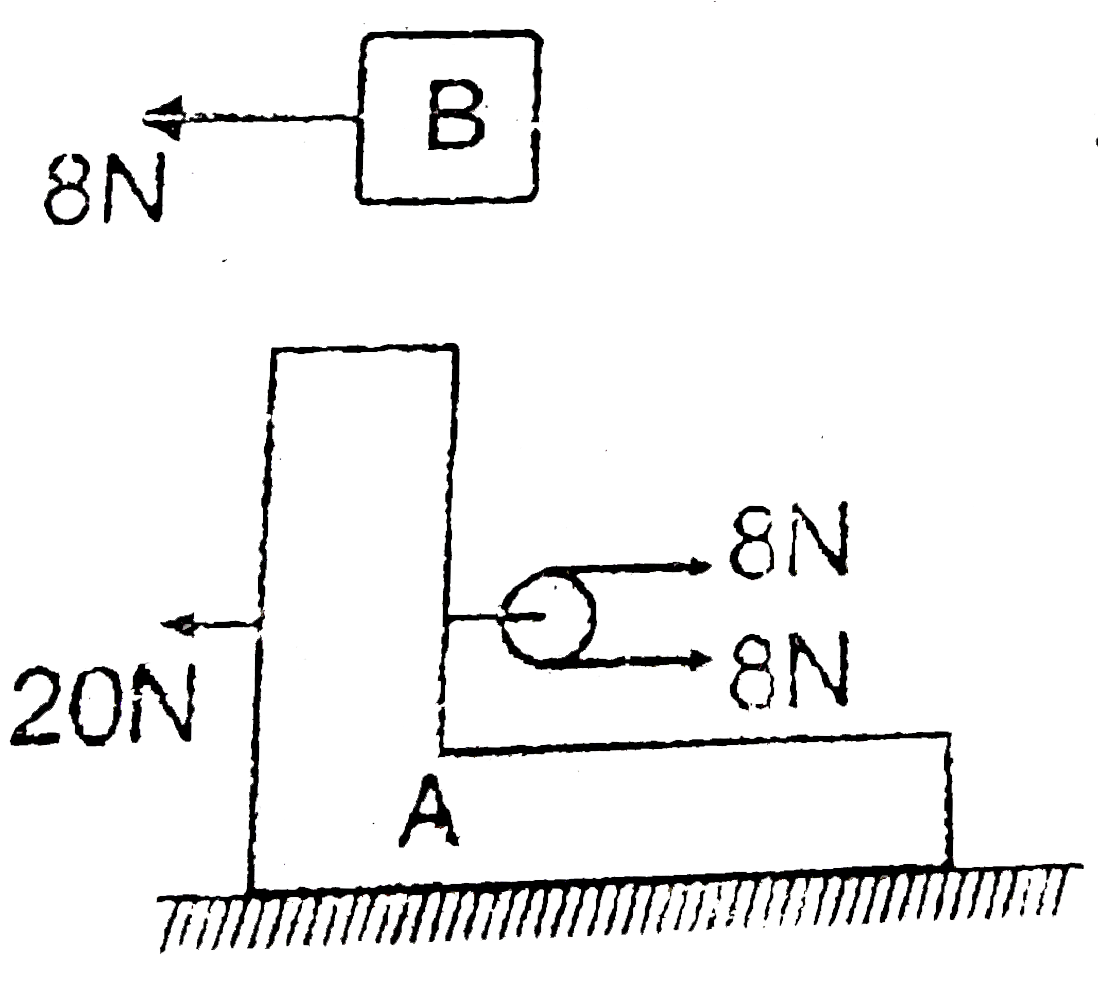Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.17|20 VideosDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.18|9 VideosDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.15|20 VideosCURRENT ELECTRICITY
RESONANCE|Exercise High Level Problems (HIP)|21 VideosELECTRO MAGNETIC WAVES
RESONANCE|Exercise Exercise 3|27 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEM-DPP No.16
- Blocks m(1) and m(2) starts from rest and move to right with accelerat...
Text Solution
|
- A smooth wedge of mass M is pushed with an acceleration a=gtantheta an...
Text Solution
|
- When photons of energy 4.25 eV strike the surface of metal A, the ejec...
Text Solution
|
- In an experiment on photoelectric effect light of wavelength 400 nm is...
Text Solution
|
- Having gone through a plank of thickness h, a bullet changed its veloc...
Text Solution
|
- A 1kg block B rests as shown on a bracket A of same mass. Constant for...
Text Solution
|
- A glass prism with a refracting angle of 60^(@) has a refractive index...
Text Solution
|
- A glass prism with a refracting angle of 60^(@) has a refractive index...
Text Solution
|
- A glass prism with a refracting angle of 60^(@) has a refractive index...
Text Solution
|