Home
Class 12
PHYSICS
Two stones are thrown vertically upwards...

Two stones are thrown vertically upwards simultaneously from the same point on the ground with initial speed `u_(1) = 30 m//sec` and `u_(2) = 50 m//sec`. Which of the curve represent correct variation (for the time interval in which both reach the ground) of
`(x_(2) - x_(1))` = the relative position of second stone with respect to first with time (t)
`(v_(2) - v_(1))` = the relative velocity of second stone with respect to first with time (t).
Assuming that stones do not rebound after hitting.

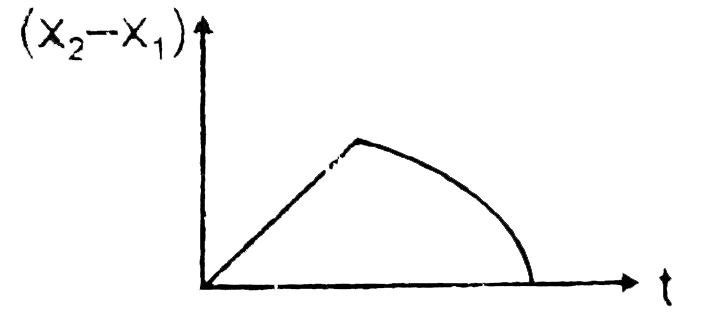
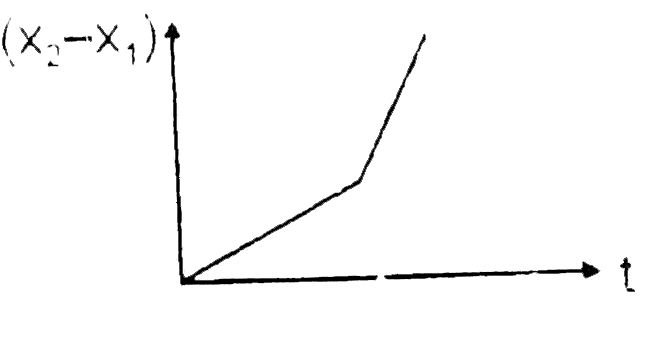
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
A, D
While both the stones are in flight `a_(1) =g` and `a_(2) =g`
So `a_("rel") = 0 rArr V_("rel")` = constant
`rArr x_("rel") =` (const) t
`rArr` Curve of `x_("rel") v//s t` will be straight line. `X_("rel")` will be straight line.
After the first particle drops on ground, the seperation `(x_("rel"))` will decrease parabolically (due to gravitational acceleration) and finally becomes zero.
and `V_("rel")` = slope of `x_("rel") v//s t`
`x_("rel") t`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEM

    RESONANCE|Exercise DPP No.19|20 Videos

  • DAILY PRACTICE PROBLEM

    RESONANCE|Exercise DPP No.20|9 Videos

  • DAILY PRACTICE PROBLEM

    RESONANCE|Exercise DPP No.17|20 Videos

  • CURRENT ELECTRICITY

    RESONANCE|Exercise High Level Problems (HIP)|21 Videos

  • ELECTRO MAGNETIC WAVES

    RESONANCE|Exercise Exercise 3|27 Videos

Similar Questions

Explore conceptually related problems

A stone is thrown upwards and it rises to a height 0f 200m. The relative velocity of the stone with respect to the earth will be maximum at :-

Two stones are thrown up simultaneously from the edge of a cliff with initial speed v and 2 v . The relative position of the second stone with respect to first varies with time till both the stones strike the ground as.

A stone is thrown vertically upwards with an initial speed u from the top of a tower, reaches the ground with a speed 3 u . The height of the tower is :

Two stones are thrown up simultaneously with initial speeds of u_(1) and u_(2)(u_(2)gt_(1) u_(1)) . They hit the ground after 6 s and 10 s respectively. Which graph in fig. correctly represents the time variation of Deltax=(x_(2)-x_(1)) the relative position of the second stone with respect to the first upto t=10 s? Assume that the stones do not rebound after hitting the ground.

A stone is thrown vertically upwards with a velocity of 4.9 ms^(-1) . Calculate : the time taken to reach the ground.

Two stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . g= 10 m//s^(2) (The figures are schematic and not drawn to scale)

Two stones are thrown up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m//s and 40 m//s respectively . Which of the following graph best represents the time variation of relative position of the speed stone with respect to the first ? ( Assume stones do not rebound after hitting the groumd and neglect air resistance , take g = 10 m//s^(2)) ( The figure are schematic and not drawn to scale )

A stone is thrown vertically upwards with a velocity of 4.9 ms^(-1) . Calculate : the velocity with which it returns to the ground.