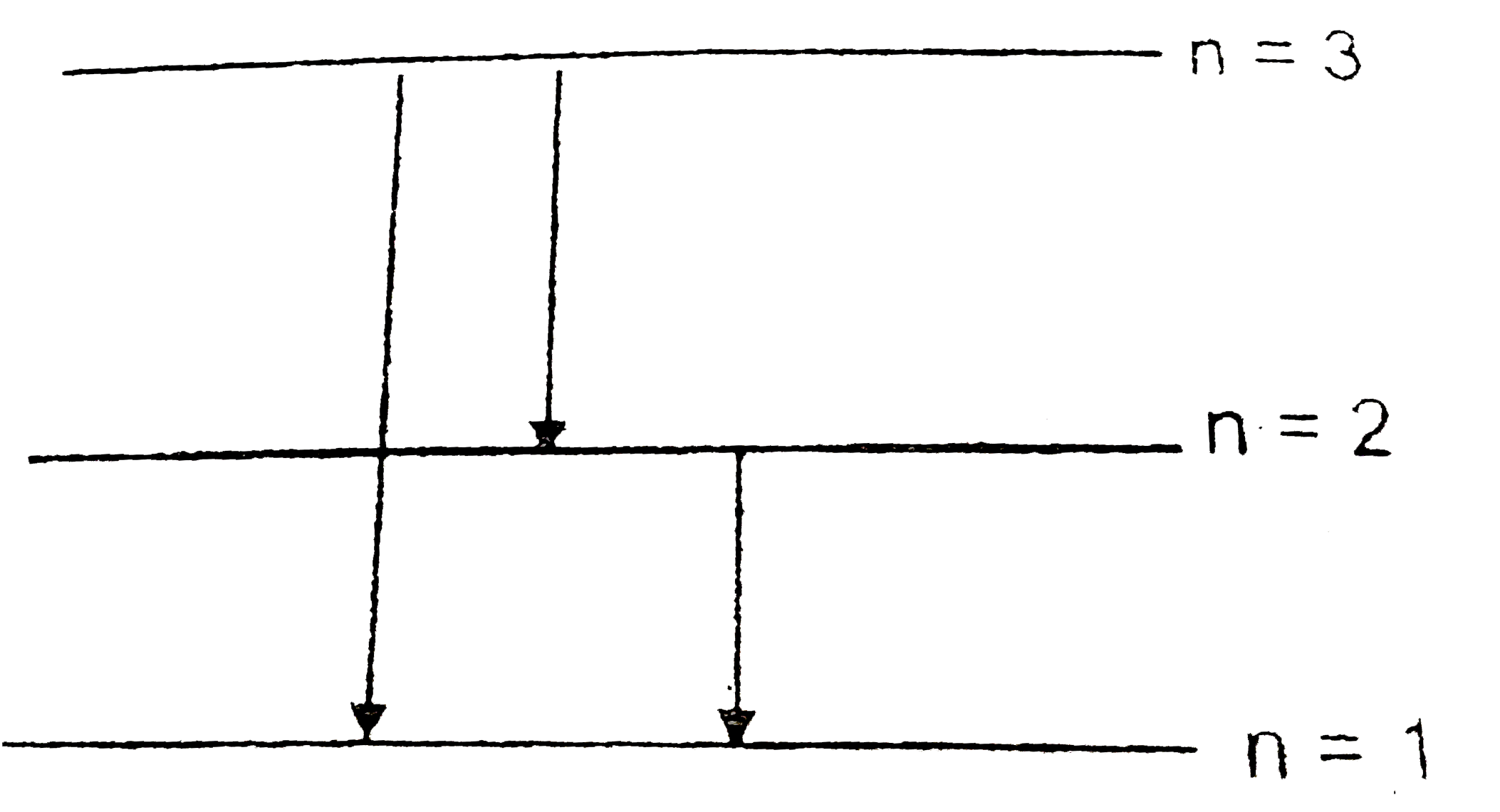
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.21|20 VideosDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.22|9 VideosDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.19|20 VideosCURRENT ELECTRICITY
RESONANCE|Exercise High Level Problems (HIP)|21 VideosELECTRO MAGNETIC WAVES
RESONANCE|Exercise Exercise 3|27 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEM-DPP No.20
- A metal is illumimated by light of two different wavelength 248nm and ...
Text Solution
|
- The radius of the orbit of an electron in a Hydrogen - like atom is 4....
Text Solution
|
- A cylinder rests in a supporting carriage as shown. The side AB of car...
Text Solution
|
- A painter is applying force himself to raise him and the box with an a...
Text Solution
|
- What is the minimum acceleration with which bar A (figure) should be s...
Text Solution
|
- Figure shows an ideal pulley block of mass m = 1 kg. resting on a roug...
Text Solution
|
- A meter stick AB of length 1 meter rests on a frictionless floor in ho...
Text Solution
|
- A meter stick AB of length 1 meter rests on a frictionless floor in ho...
Text Solution
|
- A meter stick AB of length 1 meter rests on a frictionless floor in ho...
Text Solution
|