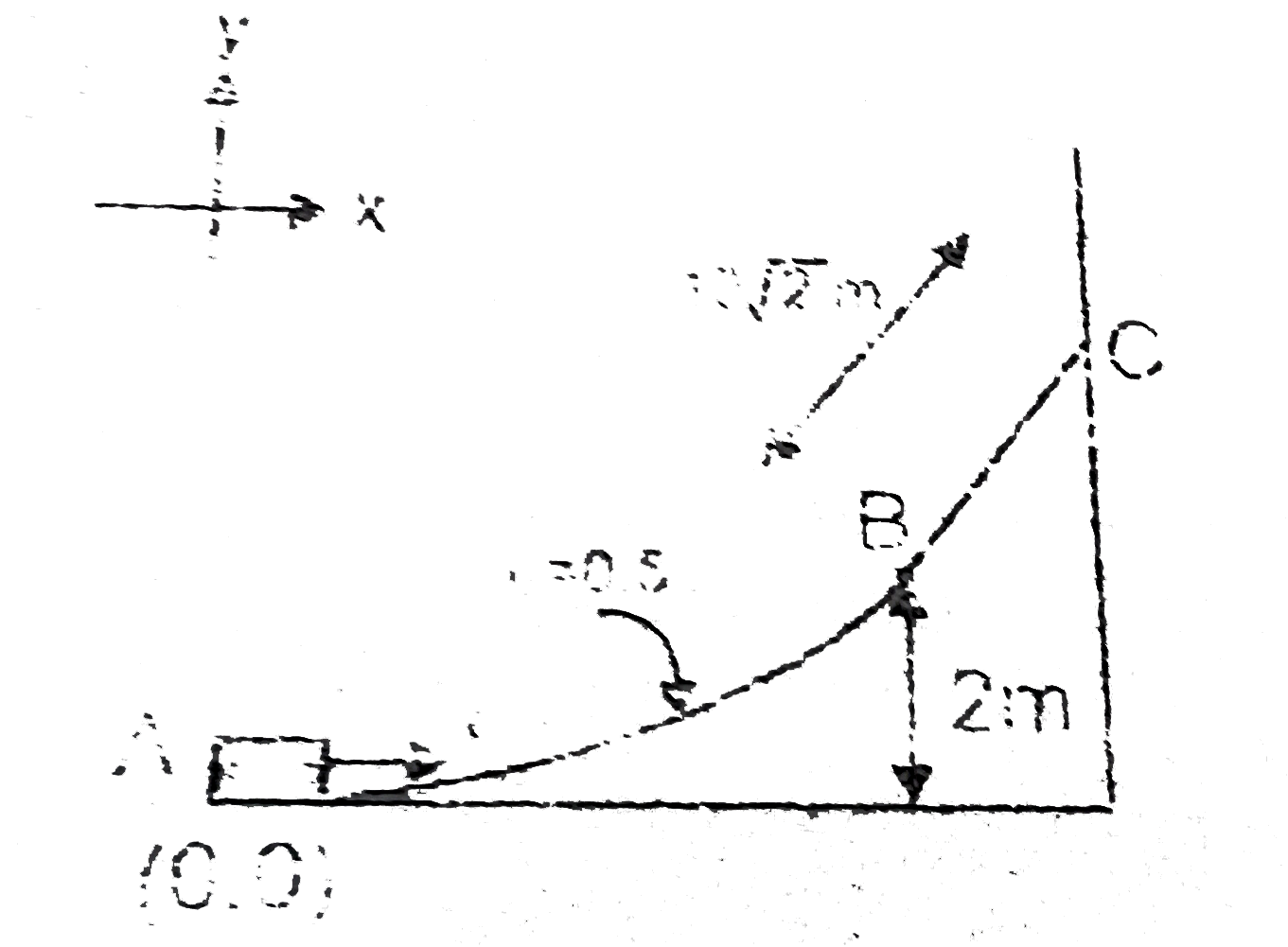Text Solution
Verified by Experts
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.25|20 VideosDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.26|9 VideosDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.23|20 VideosCURRENT ELECTRICITY
RESONANCE|Exercise High Level Problems (HIP)|21 VideosELECTRO MAGNETIC WAVES
RESONANCE|Exercise Exercise 3|27 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEM-DPP No.24
- A man starts walking on a circular track of radius R. First half of th...
Text Solution
|
- In given arrangement, 10 kg and 20 kg blocks are kept at rest on two f...
Text Solution
|
- The system shown is in limiting equilibrium. The coefficient of fricti...
Text Solution
|
- Which of the following is//are conservative force (s) ?
Text Solution
|
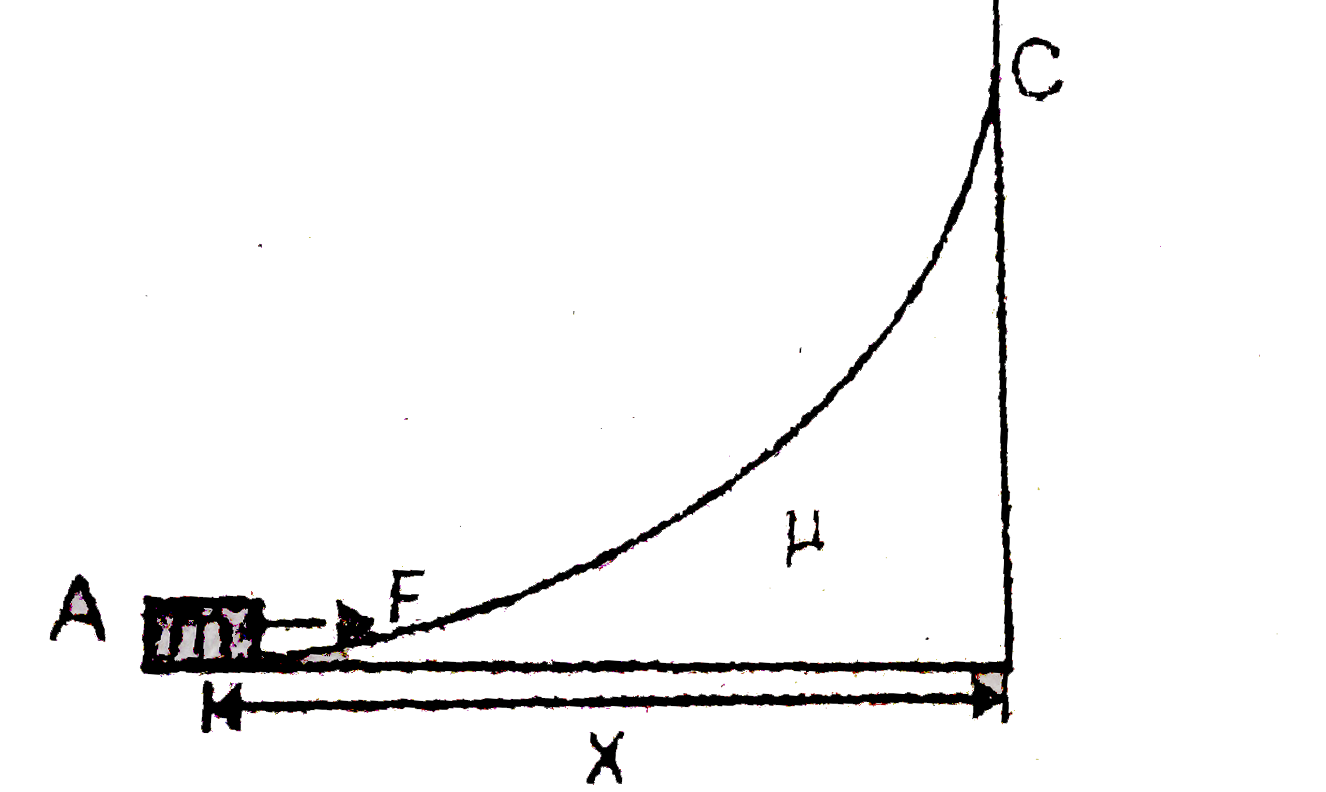
- Work done by force F to move block of mass 2 kg from A to C very slowl...
Text Solution
|
- A car moves uniformly along a horizontal since curvey = a sin (x//alph...
Text Solution
|
- When light of sufficiently high frequency is incident on a metallic su...
Text Solution
|
- When light of sufficiently high frequency is incident on a metallic su...
Text Solution
|
- When light of sufficiently high frequency is incident on a metallic su...
Text Solution
|