Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NARAYNA-VECTORS-LEVEL-II (H.W)
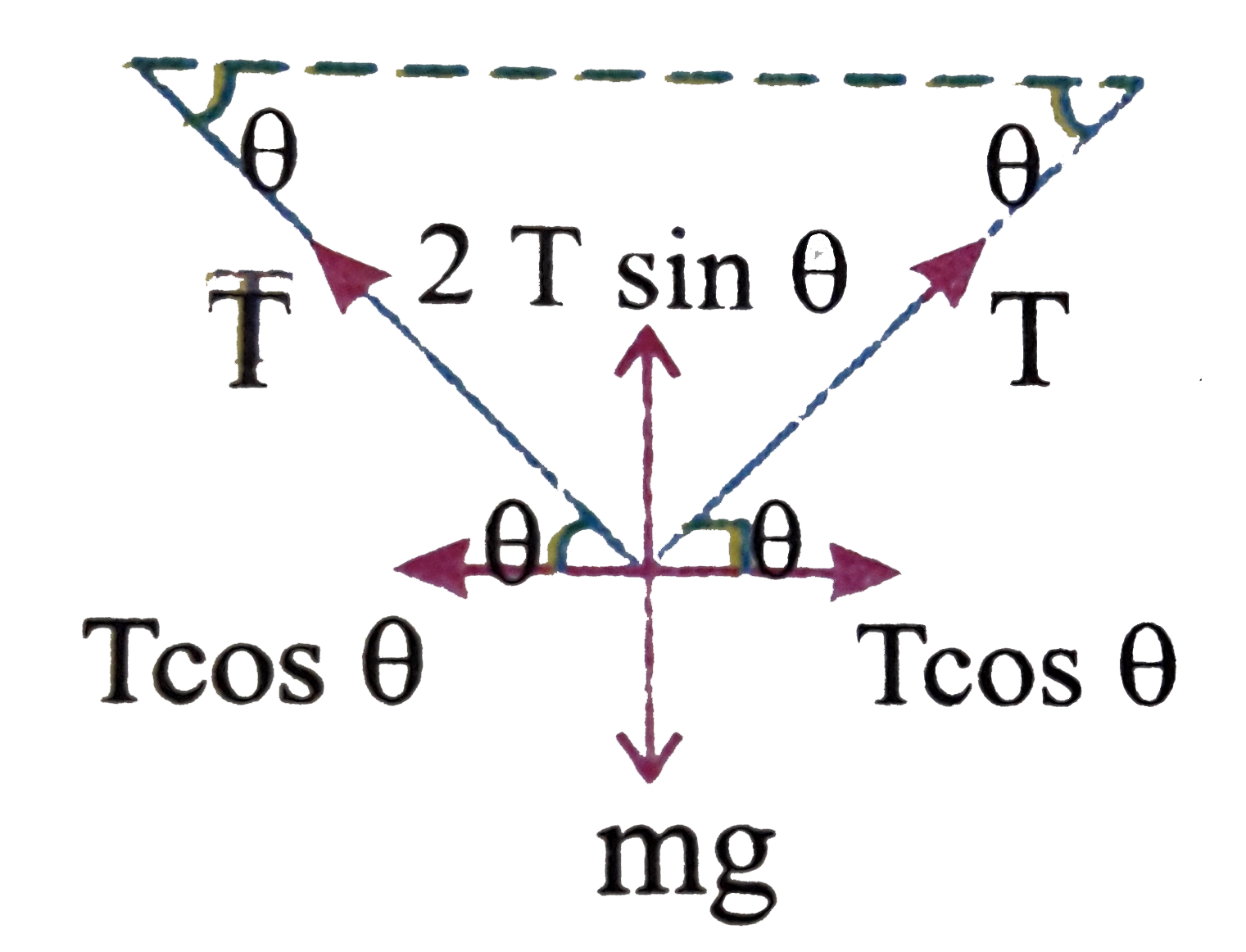
- A weight mg is suspended from the middle of a rope whose ends are at t...
Text Solution
|
- A particle has a displacement of 12 m towards east then 5 m forwards n...
Text Solution
|
- Four co-planar concurrent forces are acting on a body as shown in the ...
Text Solution
|
- O is apoint on the gournd chosen as origin. A boby first suffers a dis...
Text Solution
|
- If the two directional cosiness of a vectors are (1)/sqrt(2) and (1)/s...
Text Solution
|
- A force vecF=3hati+chatj+2hatkN acting on a particle causes a displace...
Text Solution
|
- If veca and vecb are two unit vectors such that veca+2vecb and 5veca-4...
Text Solution
|
- If vecA=9hati-7hatj+5hatk and vecB=3hati-2hatj-6hatk then the value of...
Text Solution
|
- The work done by a force 2hati-hatj+5hatk when it displaces the body f...
Text Solution
|
- The component of vecA along vecB is sqrt(3) times that of the componen...
Text Solution
|
- If vecA=(2hati+3hatj) and vecB=(hati-hatj) then component of vecA perp...
Text Solution
|
- If vecA+vecB=vecR and 2vecA+vecB is perpendicular to vecB then
Text Solution
|
- If vecA=(1)/sqrt(2)cos theta hati+(1)/sqrt(2)sin thetahatj, what will ...
Text Solution
|
- (hati+hatj)xx(hati-hatj)=
Text Solution
|
- The diagonals of a parallelogram are vecA=2hati-3hatj+hatk and vecB=-2...
Text Solution
|