Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
KAPLAN-SIMILARITY, CONGRUENCE, AND PROOFS-Multiple Choice Question
- In the diagram above, overline(JL)=overline(ON) and overline(KL)=overl...
Text Solution
|
- While working on a gerometry problem Raul determines that the angles o...
Text Solution
|
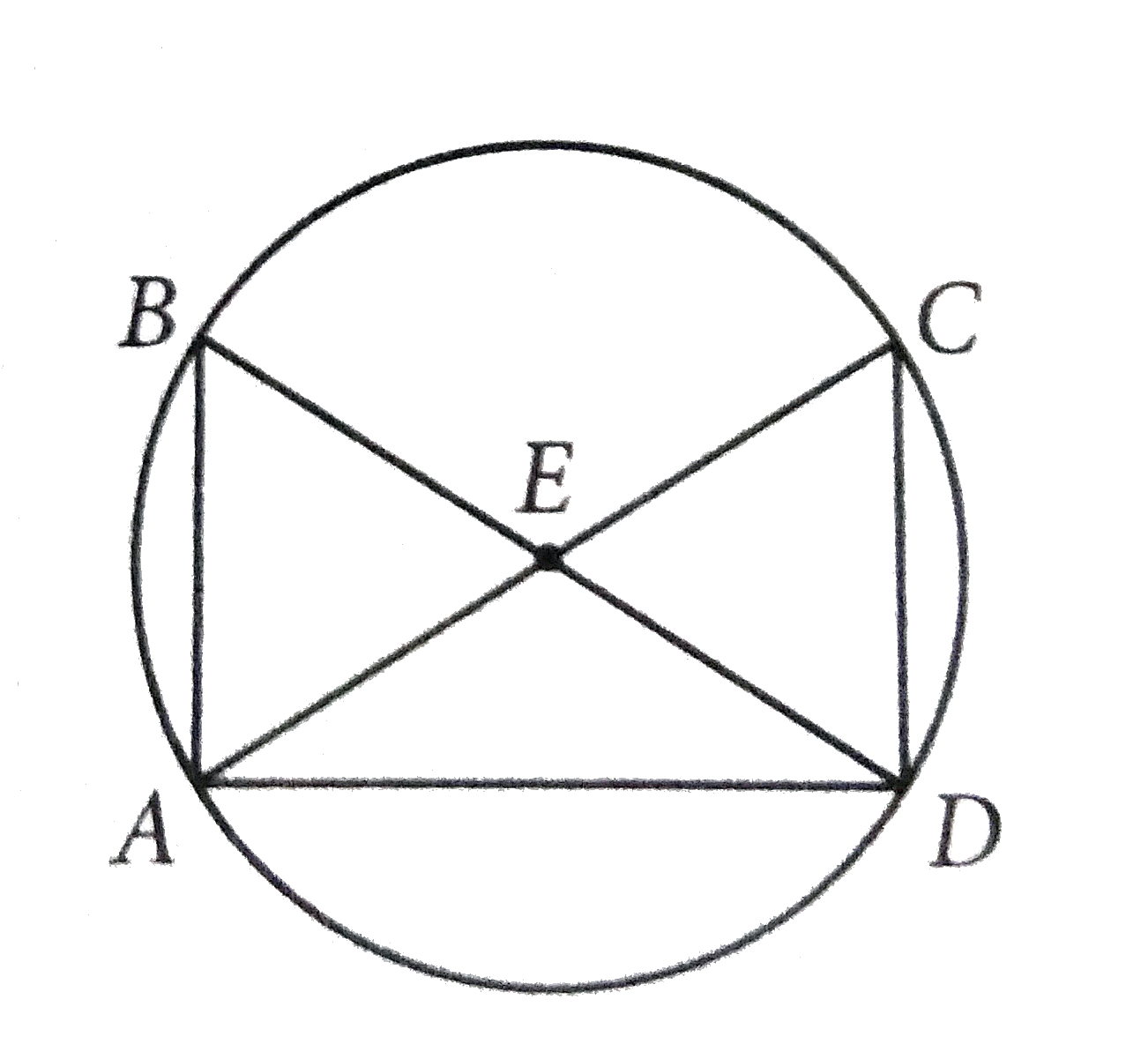
- overline(AC) and overline(BD) are diameters of circle E above. Which t...
Text Solution
|
- If the right triangle in the figure shown are similar triangle, what i...
Text Solution
|
- A triangle with side lengths of 5, 12, and 15 centimeters is similar t...
Text Solution
|
- Two triangles are graphed on a coordinate plane. Triangle MNP has vert...
Text Solution
|
- In triangle JKL above, JK=KL and JL=26. The ratio of MN to MP is 8.5. ...
Text Solution
|
- Triangle CAT is an isosceles triangle with vertices (2, 1), (6, 1), an...
Text Solution
|
- In the figure above, overline(UY) and overline(WX) are parallel and ov...
Text Solution
|
- A scientist looking at a sample of infected tissue through a microscop...
Text Solution
|