A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
FIITJEE-TEST PAPERS-PHYSICS
- A stick o fmas density lamda=8kg//m rests on a disc of radius R=20cm a...
Text Solution
|
- A bead moves along straight horizonal wire of length L, starting from ...
Text Solution
|
- Magnetic field exist in the space and given as vecB=-(B(0))/(l^(2))x^(...
Text Solution
|
- A non-conducting hollow cone has charge density sigma A path ABP is cu...
Text Solution
|
- A charge particle 'q' lies at the centre of two concentric hollow sphe...
Text Solution
|
- A point charge 'q' is placed at a distance l' (on th y-axis) verticall...
Text Solution
|
- A hollow non conducting sphere of radius R has a positive charge q uni...
Text Solution
|
- When the steady state is reached by keeping switch in position-1 then ...
Text Solution
|
- A cubical box of side 5m contains helium gas at a pressure 320 N//m^(2...
Text Solution
|
- In the given an ideal gas can change its state from A to C by two path...
Text Solution
|
- In the cylindrical region of radius R=2m, there exists a time varying ...
Text Solution
|
- A uniform conducting ring of mass m=2kg, radius r=2m and resistance 8O...
Text Solution
|
- The potential difference across a 10H inductor as a function of time i...
Text Solution
|
- Initially the switch 'S' is open for a ling time. Now the switch 'S' i...
Text Solution
|
- An electric kettle has two coils of different power. When one coil is ...
Text Solution
|
- A ideal gas whose adiabatic exponent equals gamma is expanded so that ...
Text Solution
|
- When steady state is reached, switch S is opened. Then the amount of h...
Text Solution
|
- A coil of inductance L=5H and resistance R=55Omega is connected in ser...
Text Solution
|
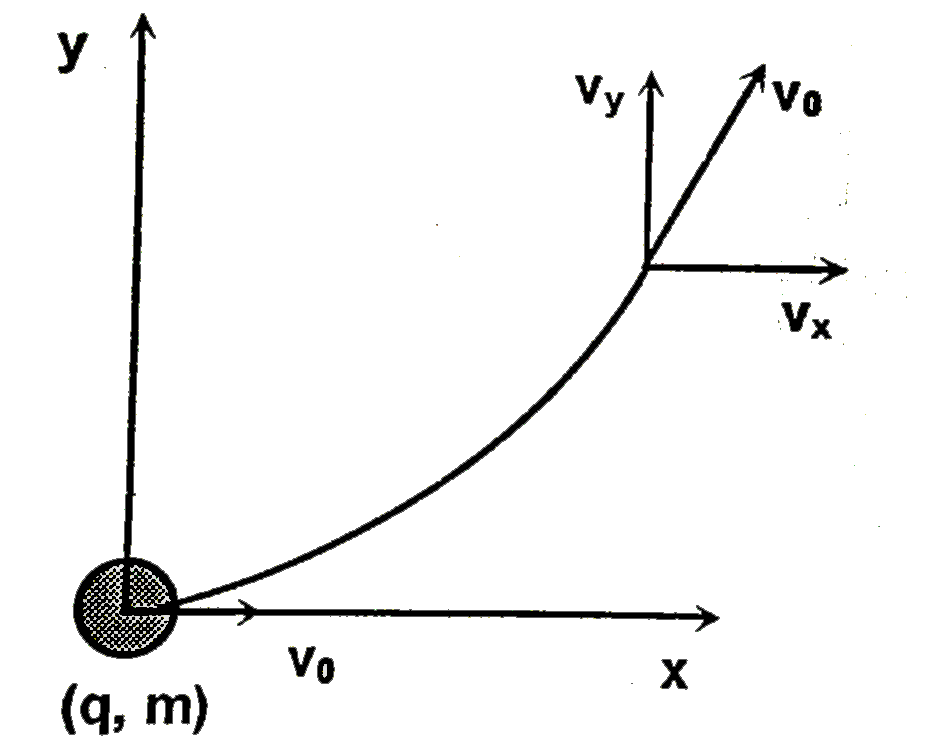
- A particle having charge 'q' and mass 'm' is projected with velocity (...
Text Solution
|
- In th circuit the key (K) is closed at t=0. Find the current in ampere...
Text Solution
|