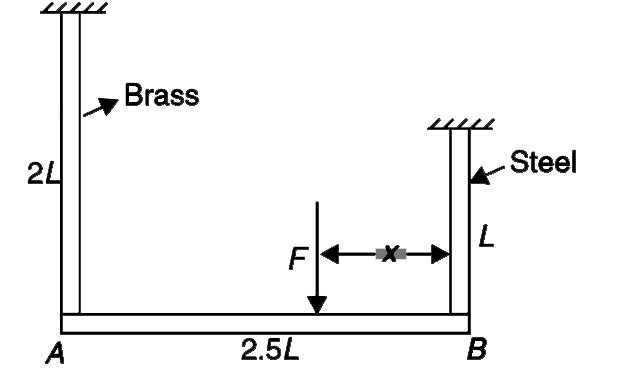
A very stiff bar (AB) of negligible mass is suspended horizontally by two vertical rods as shown in figure. Length of the bar is 2.5 L. The steel rod has length L and cross sectional radius of r and the brass rod has length 2L and cross sectional radius of 2r . A vertically downward force F is applied to the bar at a distance x from the steel rod and the bar remains horizontal. Find the value of x if it is given that ratio of Young’s modulus of steel and brass is `(Y_(s))/(Y_(B)) = 2`.