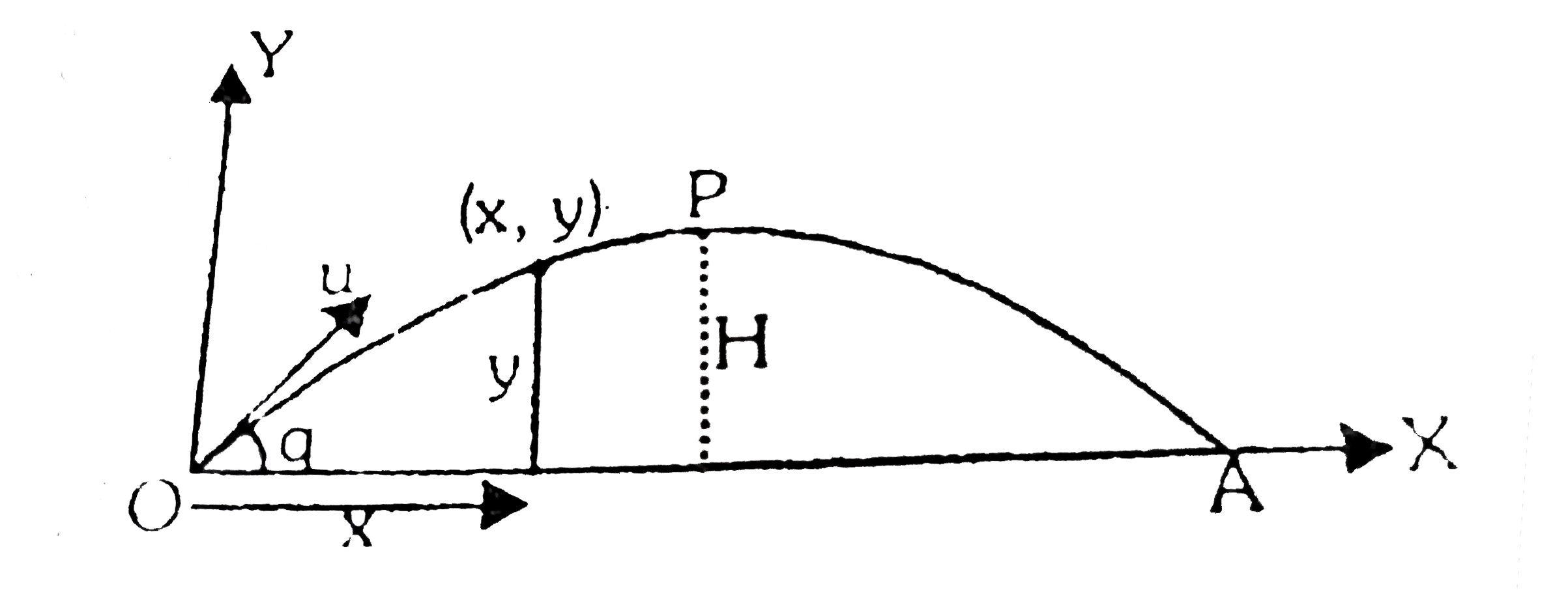Home
Class 11
PHYSICS
The trajectory of a projectile in a vert...

The trajectory of a projectile in a vertical plane is `y=sqrt(3)x-2x^(2)`. `[g=10 m//s^(2)]`

Time of flight of the projectile is :-

A

`sqrt(3/10)s`

B

`sqrt(10/3)s`

C

`1s`

D

`2s`

Text Solution

Verified by Experts

The correct Answer is:
A
Time of fight `=(2u sin theta)/g=(2xxsqrt(10)xxsqrt(3)/2)/10=sqrt(3)/10`
Promotional Banner

Topper's Solved these Questions

  • KINEMATICS

    ALLEN|Exercise Comprehension#4|3 Videos

  • KINEMATICS

    ALLEN|Exercise Comprehension#5|6 Videos

  • KINEMATICS

    ALLEN|Exercise Comprehension#2|5 Videos

  • ERROR AND MEASUREMENT

    ALLEN|Exercise Part-2(Exercise-2)(B)|22 Videos

  • KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)

    ALLEN|Exercise BEGINNER S BOX-7|8 Videos

Similar Questions

Explore conceptually related problems

The trajectory of a projectile in a vertical plane is y=sqrt(3)x-2x^(2) . [g=10 m//s^(2)] Range OA is :-

The trajectory of a projectile in a vertical plane is y=sqrt(3)x-2x^(2) . [g=10 m//s^(2)] Maximum height H is :-

The trajectory of a projectile in a vertical plane is y=sqrt(3)x-2x^(2) . [g=10 m//s^(2)] Angle of projection theta is :-

The trajectory of a projectile in a vertical plane is y=sqrt(3)x-2x^(2) . [g=10 m//s^(2)] Radius of curvature of the path of the projectile at the topmost point P is :-

The trajectory of a projectile in a vertical plane is y=ax-bx^(2) , where a and b are constants and x and y are respectively horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projection form the horizontal are:

The trajectory of a projectile in a vertical plane is y = ax - bx^2 , where a and b are constant and x and y are, respectively, horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projectile from the horizontal are.

The equation of trajectory of a projectile thrown from a point on the ground is y=(x-x^(2)/40) m. If g=10ms^(-2) The maximum height reached is

The path followed by a body projected along y axis is given by y=sqrt(3)x-(1//2)x^(2) . If g=10ms^(2) , then the initial velocity of projectile will be – (x and y are in m)

The height y and distance x along the horizontal plane of a projectile on a certain planet are given by x = 6t m and y = (8t^(2) - 5t^(2))m . The velocity with which the projectile is projected is

For ground to ground projectile motion equation of path is y=12x-3//4x^(2) . Given that g=10ms^(-2) . What is the range of the projectile ?