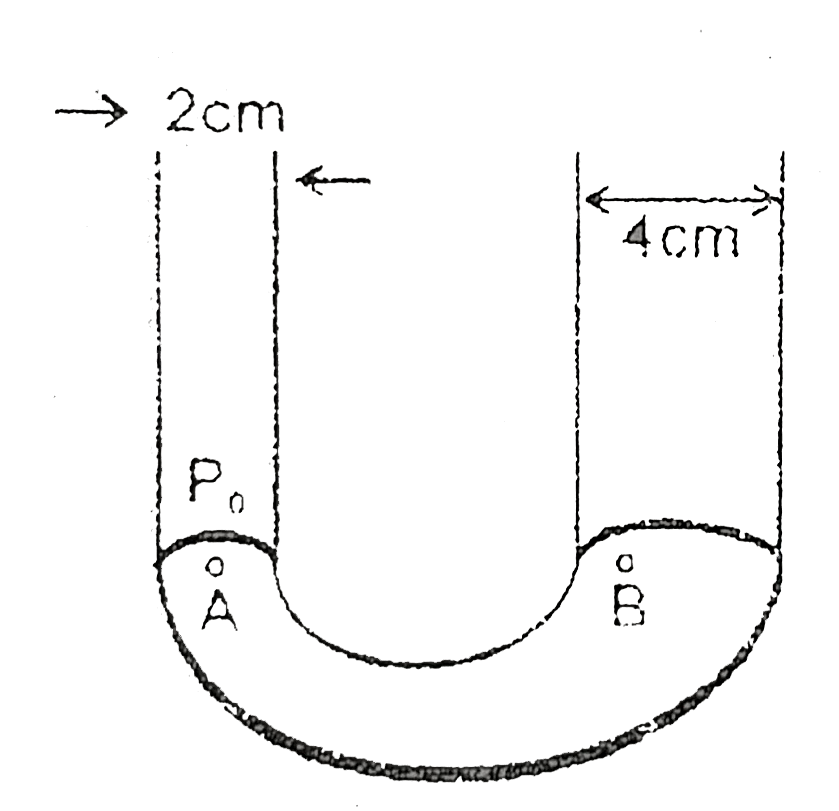Home
Class 11
PHYSICS
The interanal radius of one limb of a ca...

The interanal radius of one limb of a capillary `U-`tube is `r_(1) = 1 mm` and the internal radius of the second limb is `r_(2) = 2 mm`, the tube is filled with same mercury, and one of the limbs is connected to a vecuum pump. The surface tension & density of mercury are `480 dyn//cm` & `13.6 gm//cm^(3)` respectively (assume contact angle to be `theta = 180^(@)`)`(g = 9.8 m//s^(2)`)
Which limb of the should be connected to the pump ?

A

Limb having radius `2 mm`

B

Limb having radius `1 mm`

C

Any of the limb

D

none of these

Text Solution

Verified by Experts

The correct Answer is:
B
Pressure difference `= (2T)/(r_(1))-(2T)/(r_(2))` (`:'` angle of contact is `180^(@)`)
`rArr rho_(Hg) h_(Hg) xx g = 2T((r_(2) - r_(1))/(r_(1)r_(2)))`
`rArr h_(Hg) = (2T)/(rhog)((r_(2) - r_(1))/(r_(1)r_(2))) = 3.53 mm` of `Hg`.
As `P_(A) gt P_(B)`, althorugh they are at same height, hence the air above the point `B` has been evacuated.
So the bigger limb of the tube should be connected to the pump.
Promotional Banner

Topper's Solved these Questions

  • SURFACE TENSION

    RESONANCE|Exercise Exercise- 3 PART - I|8 Videos

  • SURFACE TENSION

    RESONANCE|Exercise Exercise- 3 PART - II|7 Videos

  • SURFACE TENSION

    RESONANCE|Exercise Exercise- 2 PART - III|3 Videos

  • STRING WAVES

    RESONANCE|Exercise Exercise|32 Videos

  • UNITS, DIMENSION & MEASUREMENT

    RESONANCE|Exercise Exercise|27 Videos

Similar Questions

Explore conceptually related problems

A capillary tube is held vertically in water . The internal radius of the tube is (1//42) cm . If the surface tension is 70 dyne /cm and angle of contact is zero , then rise in the capillary tube is

Water rises to a height fo 6 cm in a capillary tube of radius r . If the radius of the capillary tube is 3r, the height to which water will rise is ….cm.

Find the difference in levels of mercury in the limbs of a U-tube if the diameter fo bore of one limb is 1mm and of the other 4mm. The surface tension of mercury is 544 xx 10^(-3) "Nm"^(-1) its density is 13.6 xx 10^(3) "kg" m^(-3) and angle of contact is 130^(@).

Pure water rises in a capillary tube upto a height of 8 cm . If surface tension of water and acceleration due to gravity are 80 dyne/cm and 1000 cm//s^(2) respectively , then the radius of capillary tube will be

The height of liquid column in capillary tube is h the radius of capillary tube is r. rho is the density of liquid , g is acceleration due to gravity and theta is angle of contact . The surface tension of the liquid is ,

A glass capillary tube of internal radius r=0.25 mm is immersed in water. The top end of the tube projects by 2 cm above the surface of water. At what angle does the liquid meet the tube? Surface tension of water =0.7Nm^(-1) .

In the U- tube, radius of one arm is R and the other arm is 2R . Find the difference in water level if contact angle is theta = 60^(@) and surface tension of water is T .