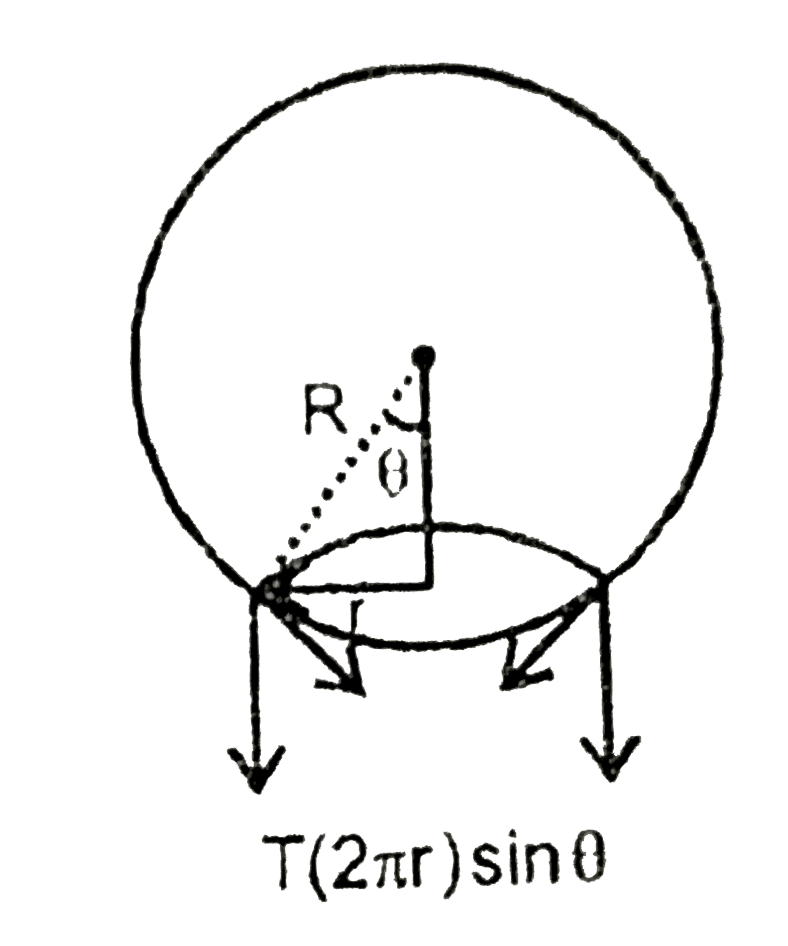
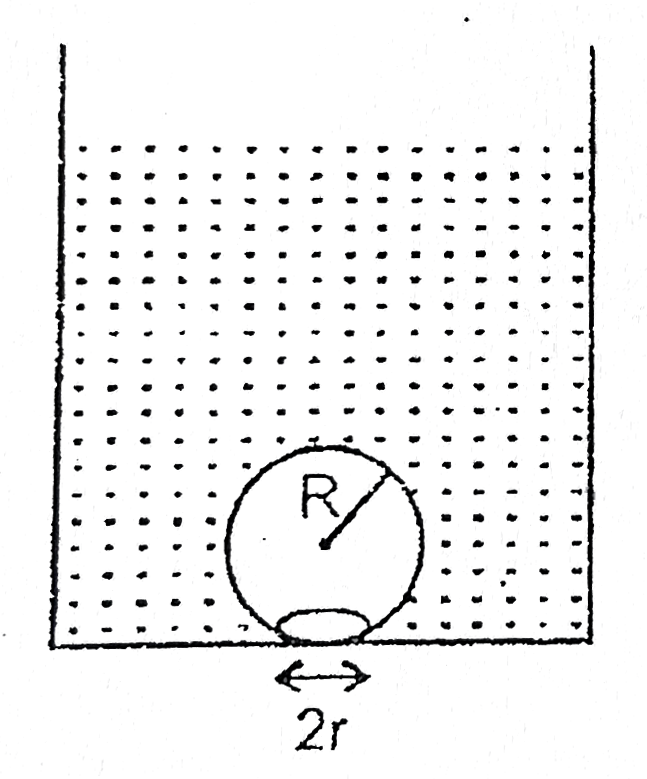A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE-SURFACE TENSION-Exercise- 3 PART - II
- A 20cm long capillary tube is dipped in water. The water rises upto 8 ...
Text Solution
|
- A capillary tube (A) is dipped in water. Another identical tube (B) is...
Text Solution
|
- Work done in increasing the size of a soap bubble from a radius of 3 c...
Text Solution
|
- Two mercury drops (each of radius 'r') merge to from bigger drop. The ...
Text Solution
|
- A thin liquid film formed between a U-shaped wire and a light slider s...
Text Solution
|
- Assume that a drop of liquid evaporates by decreases in its surface en...
Text Solution
|
- On heating water, bubbles beings formed at the bottom of the vessel de...
Text Solution
|