A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
BANSAL|Exercise EXERCISE -2 [Reasoning Type]|5 VideosGRAVITATION
BANSAL|Exercise EXERCISE -2 [Multiple Cprrect Choice Type]|15 VideosGRAVITATION
BANSAL|Exercise EXERCISE -1 [Single Correct Choice Type]|21 VideosCENTRE OF MASS & MOMENTUM CONSERVATION
BANSAL|Exercise EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)|8 VideosHEAT TRANSFER
BANSAL|Exercise Exercise|89 Videos
BANSAL-GRAVITATION-EXERCISE -2 [Paragraph Type]
- Two uniform spherical stars made of same material have radii R and 2R....
Text Solution
|
- Two uniform spherical starts made of same material have radii R and 2...
Text Solution
|
- Figure shows the orbit of a planet P round the sun S. AB and CD are th...
Text Solution
|
- Figure shows the orbit of a planet P round the sun S. AB and CD are th...
Text Solution
|
- What would happen to you frll along a straight tunnel through the cent...
Text Solution
|
- What would happen to you frll along a straight tunnel through the cent...
Text Solution
|
- What would happen to you frll along a straight tunnel through the cent...
Text Solution
|
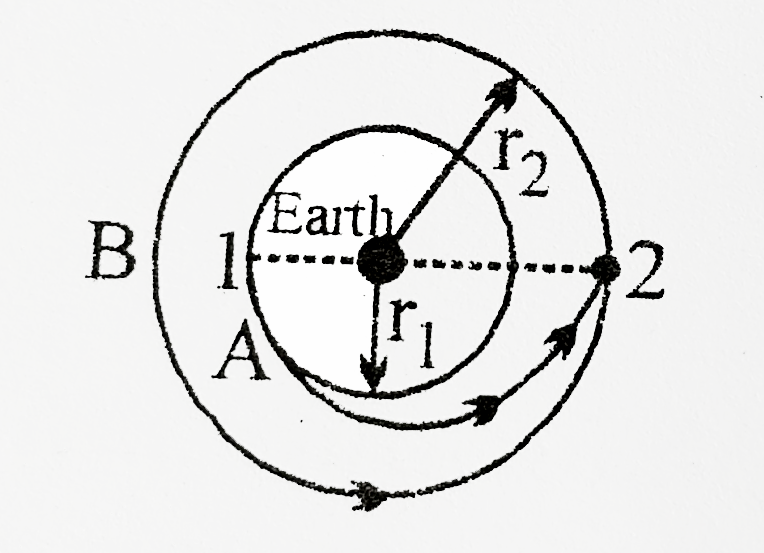
- Two satellites A and B are revolving around the earth circular orbits ...
Text Solution
|
- Two satellites A and B are revolving around the earth circular orbits ...
Text Solution
|
- Two satellites A and B are revolving around the earth circular orbits ...
Text Solution
|
- A satellite is a circular orbit radius 7000 km around the Earth. If it...
Text Solution
|