Home
Class 10
MATHS
Let A ( 4 , 2) , B ( 6 , 5) and C ( 1 ,...

Let A ( 4 , 2) , B ( 6 , 5) and C ( 1 , 4) be the vertices of `DeltaABC `
The median from A meet BC at D . Find the coordinates of the poin D . `(AS_(1))`

Text Solution

Verified by Experts

The correct Answer is:
`((6 +1)/(2),(5+4)/(2))=((7)/(2),(9)/(2))`
Promotional Banner

Topper's Solved these Questions

  • COORDINATE GEOMETRY

    VGS PUBLICATION-BRILLIANT|Exercise Think & discuss|22 Videos

  • COORDINATE GEOMETRY

    VGS PUBLICATION-BRILLIANT|Exercise Exercise 7 . 1|20 Videos

  • COORDINATE GEOMETRY

    VGS PUBLICATION-BRILLIANT|Exercise Do these|30 Videos

  • APPLICATIONS OF TRIGONOMETRY

    VGS PUBLICATION-BRILLIANT|Exercise EXERCISE|154 Videos

  • COORDINATE GEOMETRY (MULTIPLE CHOICE QUESTION)

    VGS PUBLICATION-BRILLIANT|Exercise COORDINATE GEOMETRY(MULTIPLE CHOICE QUESTION)|30 Videos

Similar Questions

Explore conceptually related problems

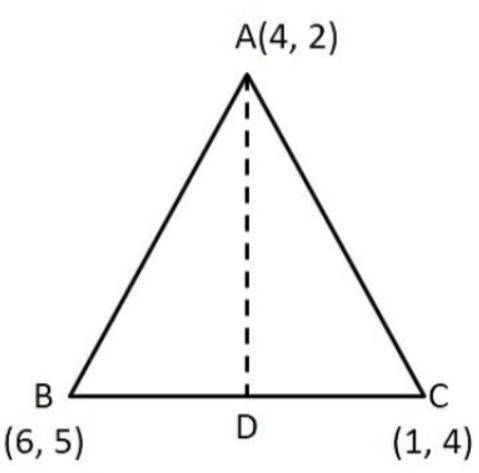
Let A(4,2) , B(6,5) and C(1,4) be the vertices of the triangleABC . The median from A meets BC at D. Find the coordinates of the point D. Find the coordinates of the point P on AD such that AP : PD = 2 : 1 .

Let A (4, 2), B(6, 5) and C(1, 4) be the vertices of DeltaABC . AD is the median on BC. Find the coordinates of the point D.

AD is the median on BC. Find the coordinates of the point D

Let A(4, 7, 8), B(2, 3, 4) and C(2,5,7) be the vertices of DeltaABC . The length of the median AD is

Let A(4,2) , B(6,5) and C(1,4) be the vertices of the △ABC. The median from A meets BC at D. Find the points which divide the line segment BE in the ratio 2 : 1 and also that divide the line segment CF in the ratio 2 : 1 .

A(0 , - 1) , B(2 , 1) and C(0 , 3) are the vertices of DeltaABC then median through B has a length .......units.

A = (2, 2), B = (6, 3), C(4, 1) are the vertices of a triangle. If D, E are the midpoints of BC, CA then DE =

LetA(4,2),B(6,5)andC(1,4)betheverticesof DeltaABC . Find the coordinates of the point Pon AD such that AP : PD = 2 : 1.

If A(1,2) , B(3,4) and C(6,6) are the three vertices of a parallelogram ABCD , find the co-ordinates of the fourth vertex D.