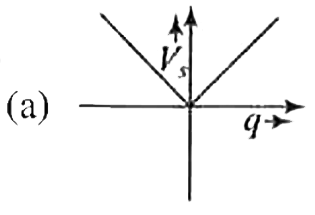
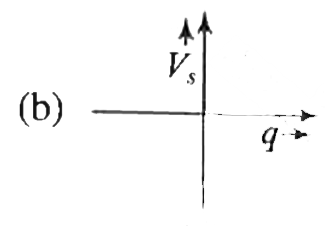
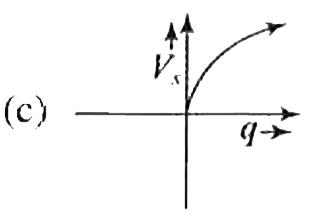
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-ELECTRIC POTENTIAL-DPP 3.4
- Two charges -q each are separated by distance 2d. A third charge +q is...
Text Solution
|
- A positively charged particle is released from rest in a uniform elect...
Text Solution
|
- If identical charges (-q) are placed at each corner of a cube of side ...
Text Solution
|
- Two charges q(1) and q(2) are placed 30 cm apart, as shown in the figu...
Text Solution
|
- A charged particle of charge 'Q' is held fixed and another charged par...
Text Solution
|
- A very large sphere having charge Q uniformly distributed on the surfa...
Text Solution
|
- In the figure shown the elctric potential energy of the system is : (q...
Text Solution
|
- A point charge 'Q' is placed at the centre of a spherical cavity of ra...
Text Solution
|
- Four charges are rigidly fixed along the Y-axis as shown. A positive c...
Text Solution
|
- Three charge +q, -q, and +2q are placed at the vertices of a right ang...
Text Solution
|
- Three equal charges Q are placed at the three vertices of an equilater...
Text Solution
|
- You are moving a negative charge q lt 0 at a small constant speed away...
Text Solution
|
- A negative charge Q is distributed uniformly in volume of a sphere is ...
Text Solution
|
- A positive point charge +Q is fixed in space .A negative point charge ...
Text Solution
|
- Small identical balls with equal charges are fixed at the vertices of ...
Text Solution
|