A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MARVEL PUBLICATION-FORCE, WORK AND TORQUE-TEST YOUR GRASP
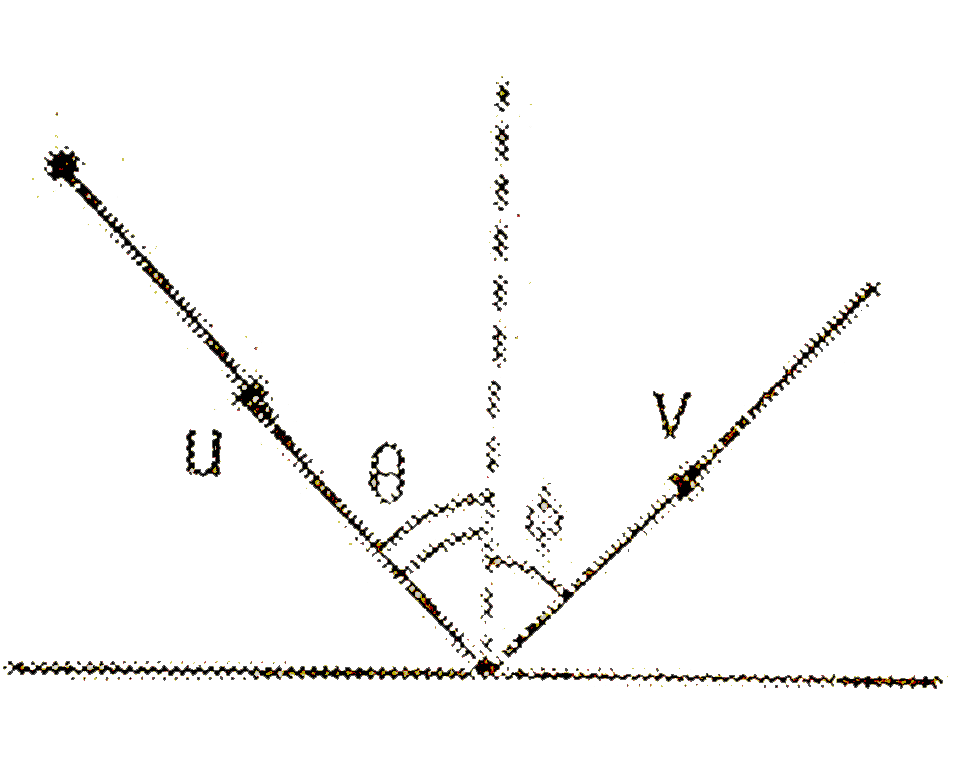
- A particle strikes a horizontal frictionless floor with a speed u, at ...
Text Solution
|
- A ball of mass 500 gram strikes a wall with a velocity of 80 m/s and ...
Text Solution
|
- A spring balance is attached to the ceiling of a lift. A man hangs his...
Text Solution
|
- Liquid fuel is burnt in a rocket and its exhaust gas is rejected from ...
Text Solution
|
- Two masses m(1) = 5 kg and m(2) = 4.8 kg tied to a string are ha...
Text Solution
|
- A particle constrained to move along the Y axis of a coordinate s...
Text Solution
|
- A light body and a heavy body have same linear momentum. Which one has...
Text Solution
|
- An electric pump is used to pump water to fill a water tank of volu...
Text Solution
|
- A body dropped form a certain height strikes the ground and rises to ...
Text Solution
|
- A metre scale is supported on a wedge at its centre of gravity. A body...
Text Solution
|
- A force vec(F) = (hati + 3 hatj) N acts on a body at a point P , wh...
Text Solution
|