Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT
PHYSICS GALAXY - ASHISH ARORA|Exercise Practice Exercise 5.2|14 VideosELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT
PHYSICS GALAXY - ASHISH ARORA|Exercise Practice Exercise 5.3|13 VideosELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT
PHYSICS GALAXY - ASHISH ARORA|Exercise Illustration|25 VideosCURRENT ELECTRICITY
PHYSICS GALAXY - ASHISH ARORA|Exercise All Questions|389 VideosELECTROSTATICS
PHYSICS GALAXY - ASHISH ARORA|Exercise Unsolved Numberical Problems|73 Videos
Similar Questions
Explore conceptually related problems
PHYSICS GALAXY - ASHISH ARORA-ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT-Practice Exercise 5.1
- A coil of area 500cm^(2) and having 1000 turns is held perpendicular t...
Text Solution
|
- Two long parallel conducting horizontal rails are connected by a condu...
Text Solution
|
- A very small circular loop of area 5xx10^(-4)m^(2) , resistance 2Omega...
Text Solution
|
- A flat circular coil having N turns (tightly wound D) is placed in a t...
Text Solution
|
- Two long parallel horizontal rails a, a distance d aprt and each havin...
Text Solution
|
- A wire frame of area 3.92xx10^(-4)m^(2) and resistance 20Omega is susp...
Text Solution
|
- A square frame with side a and a long straight wire carrying a current...
Text Solution
|
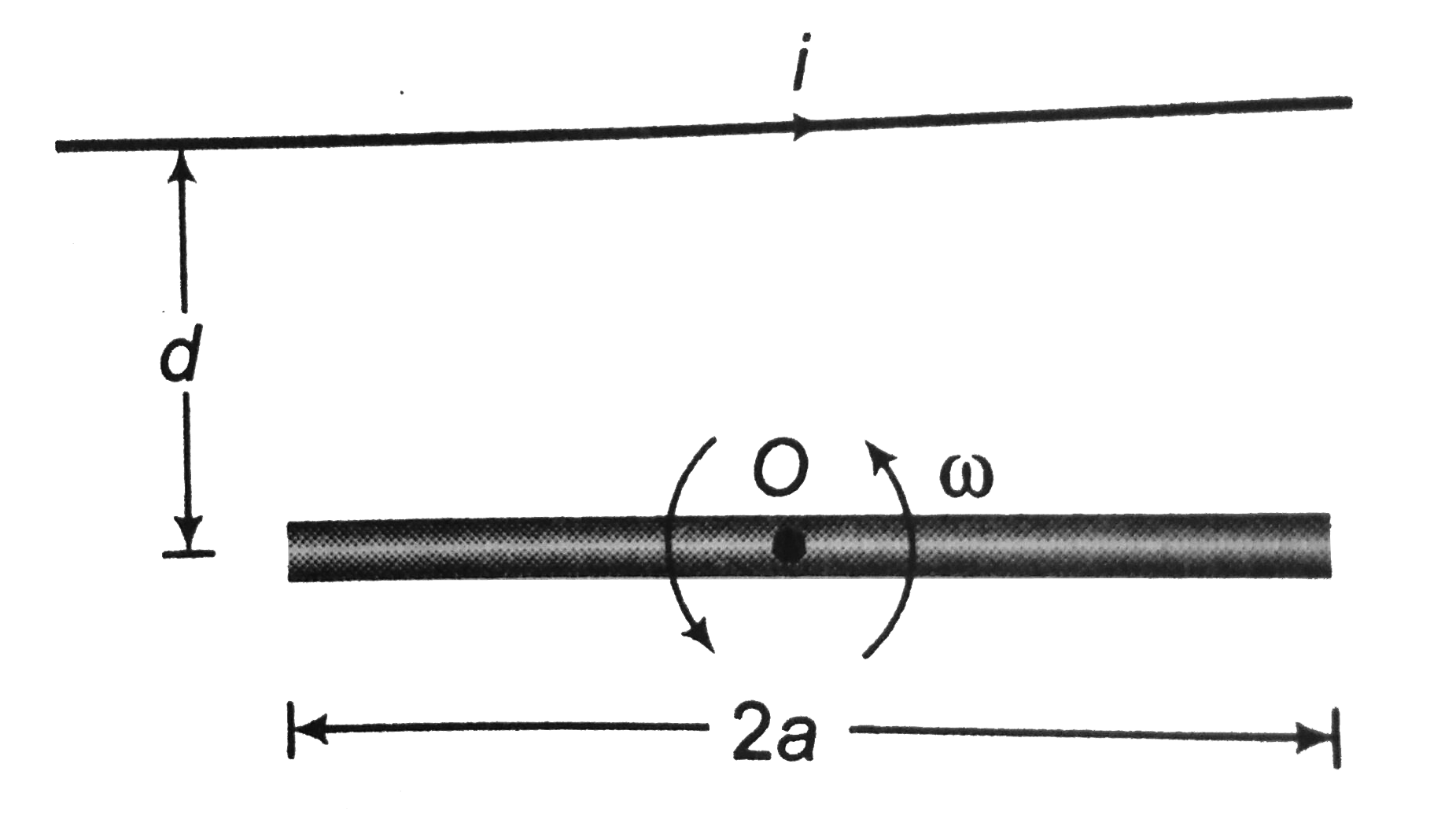
- A rod of length 2a is free to rotate in a vertical plane, about a hori...
Text Solution
|
- Two long wires are placed on a pair of parallel rails perpendicular to...
Text Solution
|
- A uniform rod AB of mass m and length l is placed over two smooth con...
Text Solution
|
- In figure-5.54 a wire ring of radius R is in pure rolling on a surface...
Text Solution
|
- Figure-5.55 shows a small circular coil of area A suspended from a poi...
Text Solution
|