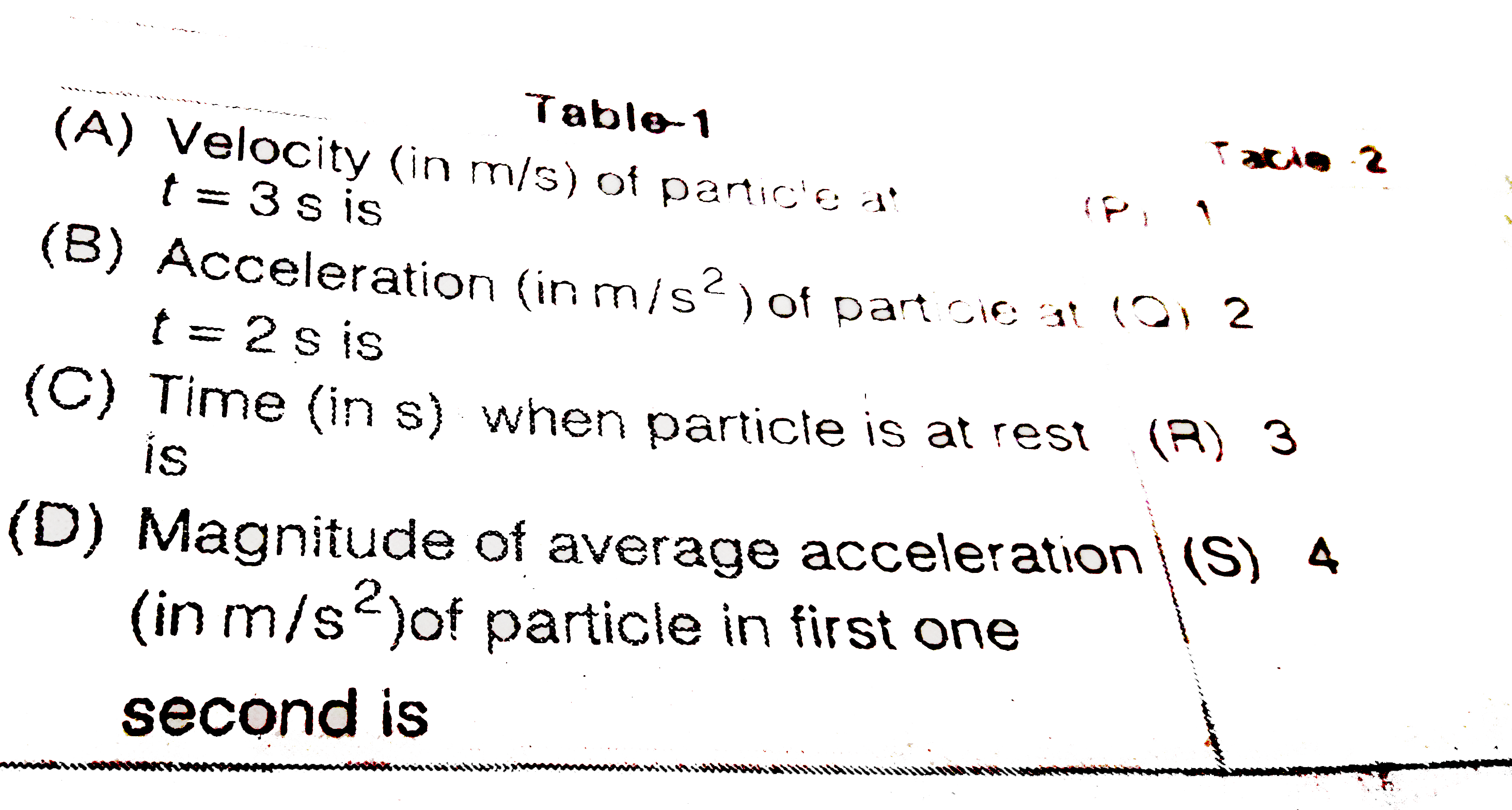Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY-KINEMATICS 1-MATCH THE COLUMN
- Match the following Table-1 to Table-2
Text Solution
|
- Velocity of a particle is in negative direction with constant accelera...
Text Solution
|
- For the velocity -time graph shown in figure, in a time interval from ...
Text Solution
|
- Let us call a motion, A when velocity is positive and increasing A^(-1...
Text Solution
|
- In the s-t equations (s=10+20t-5t^(2)) match the following
Text Solution
|
- Match the following
Text Solution
|
- A balloon rises up with constant net acceleration of 10 m//s^(2). Afte...
Text Solution
|
- Table -1 gives some graph for a particle moves along x-axis in positiv...
Text Solution
|
- Velocity (in m/s) of a particle moving in a straight line given by v=(...
Text Solution
|
- A ball of mas 2gm is thrown vertically upwards with a speed of 30m//s ...
Text Solution
|