Home
Class 11
PHYSICS
A particle of mass = 2kg moves in simple...

A particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is `(npi)/5` second. Find value of n.

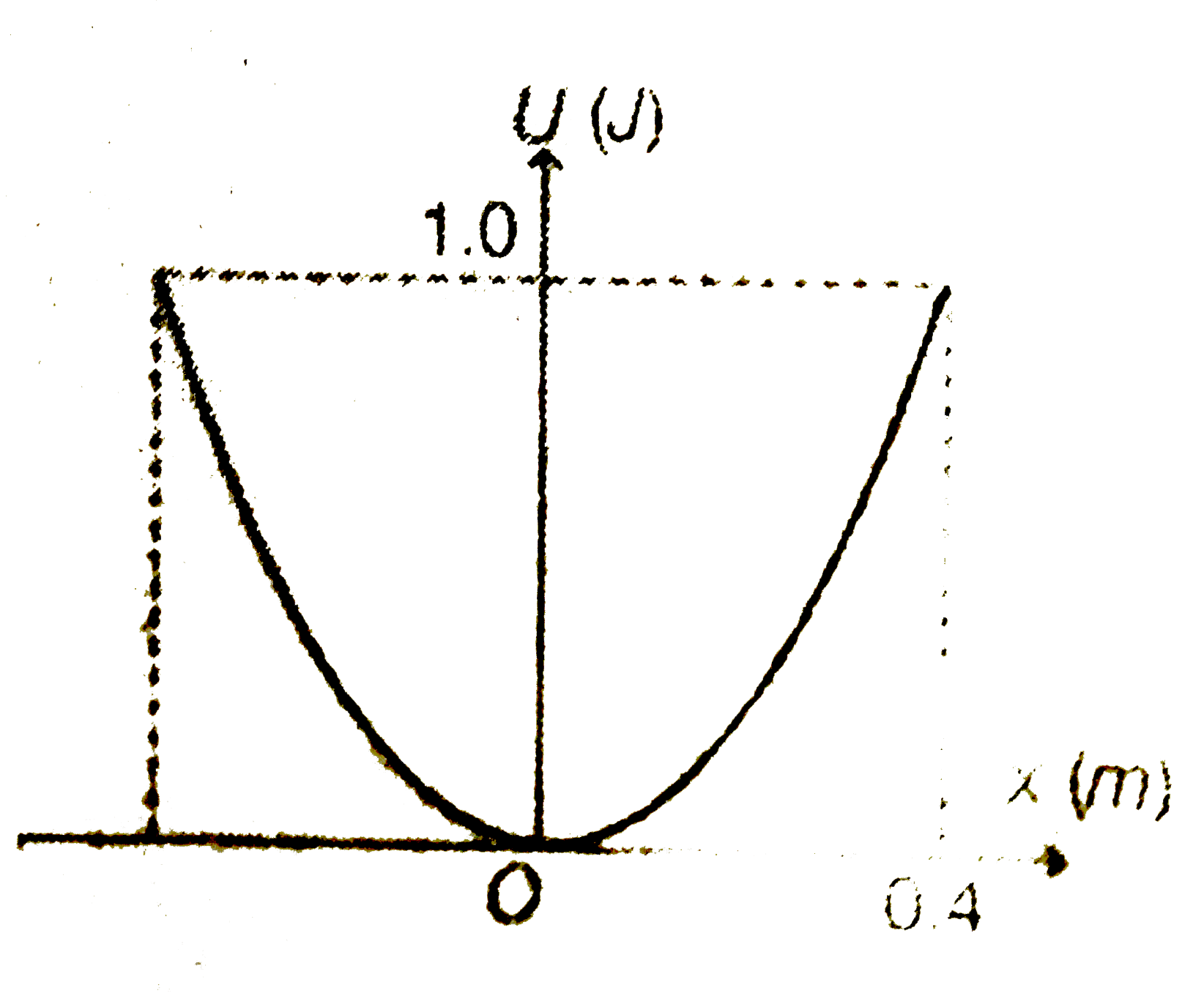
Text Solution

Verified by Experts

The correct Answer is:
4
Promotional Banner

Topper's Solved these Questions

  • SIMPLE HARMONIC MOTION

    DC PANDEY|Exercise Matrix matching type questions|13 Videos

  • SEMICONDUCTORS AND ELECTRONIC DEVICES

    DC PANDEY|Exercise More than One Option is Correct|3 Videos

  • SOLVD PAPERS 2017 NEET, AIIMS & JIPMER

    DC PANDEY|Exercise Solved paper 2018(JIPMER)|38 Videos

Similar Questions

Explore conceptually related problems

A particle of mass 2 kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

A particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is :-

A particle of mass 0.2 kg moves with simple harmonic motion of amplitude 2 cm. If th~ total energy of the particle is 4 xx10^(-5) J, then the time period of the motion is

A particle of mass m= 5g is executing simple harmonic motion with an amplitude 0.3 m and time period pi//5 second. The maximum value of force acting on the particle is

When a particle oscillates simple harmonically, its potential energy varies periodically. If the frequency of oscillation of the particle is n, the frequency of potential energy variation is

A particle of mass m moves in the potential energy U shoen above. The period of the motion when the particle has total energy E is

A particle of mass 3 kg , attached to a spring with force constant 48Nm^(-1) execute simple harmonic motion on a frictionless horizontal surface. The time period of oscillation of the particle, is seconds , is

When a particle oscillates in simple harmonic motion, both in potential energy and kinetic energy vary sinusoidally with time. If v be the frequency of the motion of the particle, the frequency associated with the kinetic energy is :