Home
Class 11
PHYSICS
A rod OA rotates about a horizontal axis...

A rod OA rotates about a horizontal axis through O with a constant anti-clockwise velocity `omega=3 rad//s.` As it pases the positions `theta=0^(@)` a small block of mass m is placed on it at a radial distacne r=450 mm If the block is observed to slip at `theta=50^(@)` the coefficient of static friction bewteen the block and the rod is (Given that ,`sin50^(@)=0766,cos 50^(@)=0.64`)

A

`0.2`

B

`0.55`

C

`0.8`

D

1

Text Solution

Verified by Experts

(d) At the time of slipping maxnimum friction acts on the body

in the frame of rod,
`mg sin theta=muN+mr omega^(2)`
Also, " " `N-mg cos theta`
`:. " " mg sin theta=mumgcostheta+mromega^(2)`
`Here, " " r=0.4.5m, theta=50^(@)`
`sin50^(@)=0.766 "and " cos 50^(@)=0.64`
`:.mu=(mgsintheta-mromega^(2))/(mg costheta)=(gsintheta-romega^(22))/(gcostheta)=0.55`
Promotional Banner

Topper's Solved these Questions

  • CIRCULAR MOTION

    BITSAT GUIDE|Exercise BITAST Archives|5 Videos

  • ELASTICITY

    BITSAT GUIDE|Exercise BITSAT ARCHIVES|9 Videos

Similar Questions

Explore conceptually related problems

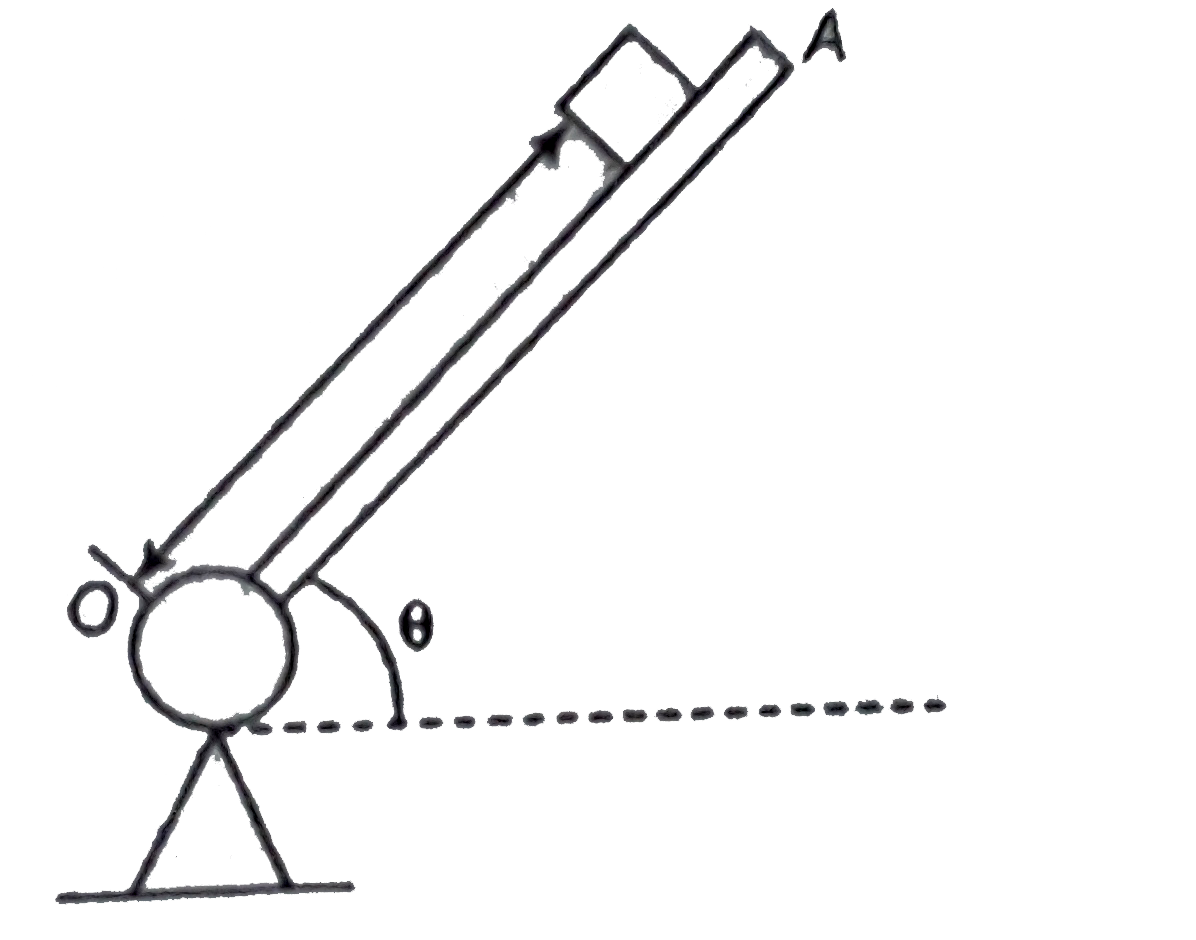
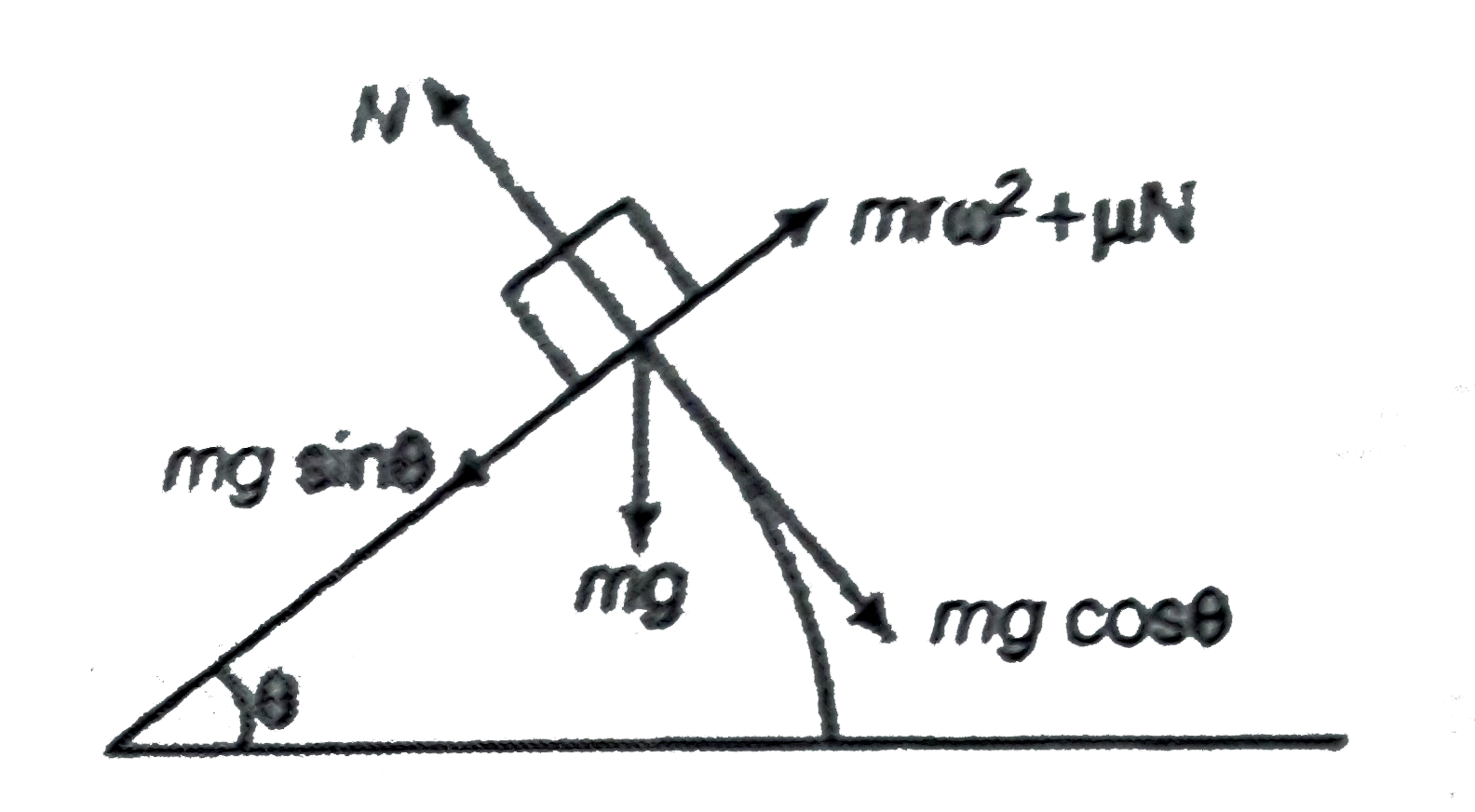
A rod OA rotates about a horizontal axis through O with a constant aniclockwise velocity omega = 3 red s^(-1) . As it passes the position theta = 0 , a small block of mass m is placed on it at a radial distance r = 450 mm if the block is observed to slip at theta = 50^(@) . Find the coefficient of static friction between the block and the rot (Given that sin 50^(@) = 0.766, cos 50^(@) = 0.64)

The inclined plane OA rotates in vertical plane about a horizontal axis through O with a constant counter clockwise velocity omega=3 rad/sec. As it passes the position theta=0 , a small m=1 kg is placed upon it at a radial distance r=0.5 m. if the mass is observed to be at rest with respect to inclined plane. The value of static friction force at theta=37^(@) between the mass and the incline plane

A homogeneous disc of weight W and radius R rotates about the vertical axis OZ, the initial angular velocity being omega_(0) . During the motion, the brake block A is pressed to the disc,with a radial force N for t_(0) seconds and the disc comes to rest because of friction. Find the coefficient of friction.

A block of mass 50 kg slides over a horizontal distance of 1m. If the coefficient of friction between their surface is 0.2, then work done against friction is (take g = 9.8 m//s^(2) ) :

A cubical block of mass M vibrates horizontally with amplitude of 4.0 cm and a frequency of 2.0 Hz. A small block of mass is placed on the bigger block. In order that the smaller block does not side on the bigger block, the minimum value of the coefficient of static friction between the two blocks is (0.16x). Find the valule of x(Take pi^(2) =10 and g=10m/ s^(2) )

A disc of radius 4m is rotating about its fixed centre with a constant angular velocity 2(rad)/(s) (in the horizontal plane).A block is also rotating with the disc without slipping. If co-efficient of friction between the block and the disc is 0.4 ,then the maximum distance at which the block can rotate without

A rod AB of length 2m is hinging at point A and its other end B is atteched to a platform on which a point of mass m is kept. Rod rotates about point A maintaing angle theta = 30^(@) with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path.If the coeffiicent of staic friction between the block and platform is mu = 0.1 then find the maximum angular velocity in rad s^(-1) of rod so that the block does not slip on the plateform (g = 10 ms^(-2))

A block of mass m is kept on the edge of a horizontal turn table of radius R which is rotating with constant angular verticle omega (along with the block ) about its axis . If coefficient of friction is mu , find the friction force between block and table.