Home
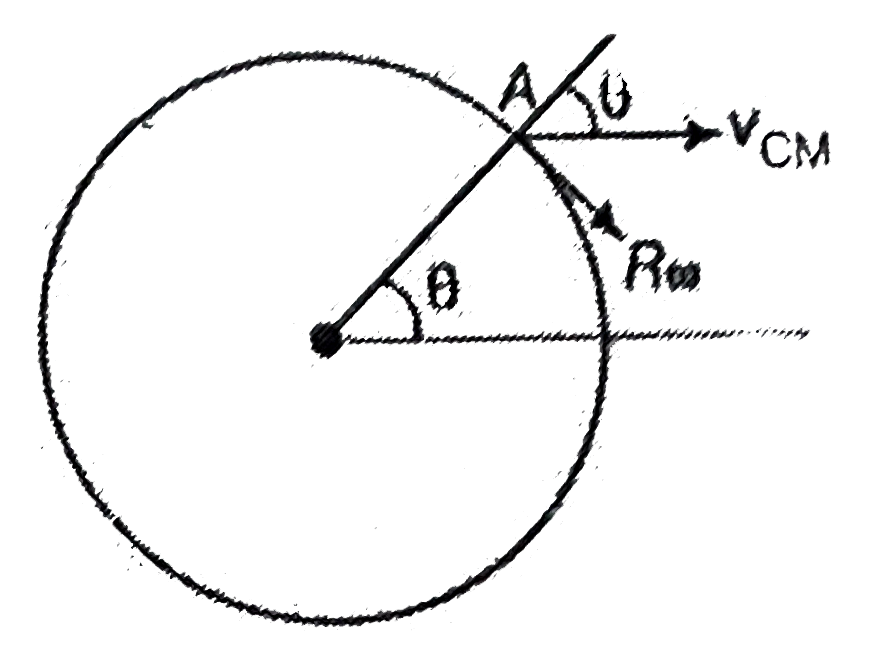
Class 11
PHYSICS
A sphere of radius R is rolling on a rou...

A sphere of radius R is rolling on a rough horizontal surface. The magnitude of velocity of A with respect to ground will be

A

`sqrt(2)v_(CM)`

B

2`V_(CM)sintheta`

C

`sqrt(2)v_(CM)sqrt(1+sintheta)`

D

No sufficient information

Text Solution

Verified by Experts

c) Here `v_(CM) = Romega`
`The resultant velocity of point A is
`v_(A) = sqrt(v_(CM)^(2) + (Romega)^(2) + 2v_(CM)(Romega)cos(90-theta))`
`=sqrt(v_(CM)^(2) + v_(CM)^(2) + 2v_(CM)^(2)sintheta)`
`sqrt(2)v_(CM)sqrt(1+sintheta))`
Promotional Banner

Topper's Solved these Questions

  • ROTATIONAL MOTION

    BITSAT GUIDE|Exercise BITSAT Archives|9 Videos

  • NEWTONS LAWS OF MOTION AND FRICTION

    BITSAT GUIDE|Exercise BITSAT Archives|23 Videos

  • SCALARS AND VECTORS

    BITSAT GUIDE|Exercise All Questions|34 Videos

Similar Questions

Explore conceptually related problems

A disc is rolling on a rough horizontal surface. The instantaneous speed of the point of contact during perfect rolling is zero with respect to ground. The force of friction can help in achieving pure rolling condition.

A uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : at the upper most point

A uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : the centre of mass

A uniform solid sphere of radius R , rolling without sliding on a horizontal surface with an angular velocity omega_(0) , meets a rough inclined plane of inclination theta = 60^@ . The sphere starts pure rolling up the plane with an angular velocity omega Find the value of omega .

A ring of radius R rolls without slipping on a rough horizontal surface with a constant velocity. The raduius of curvature of the path followed by any particle of the ring at the highest point of its path will be : .

A disc of radius R is moving on a rough horizontal surface with velocity v and angular speed omega at an instant as shown in figure. Choose the correct statement.

A sphere is performing pure rolling on a rough horizontal surface with constant angular velocity. Frictional force acting on the sphere is zero. Velocity of contact point is zero.