A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SYSTEMS OF LINEAR EQUATIONS
KAPLAN|Exercise SUBSTITUTION|1 VideosSYSTEMS OF LINEAR EQUATIONS
KAPLAN|Exercise COMBINATION|1 VideosSYSTEMS OF LINEAR EQUATIONS
KAPLAN|Exercise ON TEST DAY|1 VideosSCATTERPLOTS
KAPLAN|Exercise SCATTERPLOT MODELING|1 VideosTHE MATHOD OF SAT MATH QUESTIONS
KAPLAN|Exercise TRY ON YOUR OWN|10 Videos
Similar Questions
Explore conceptually related problems
KAPLAN-SYSTEMS OF LINEAR EQUATIONS-HOW MUCH HAVE YOU LEARNED
- If 8x-2y=10 and 3y-9x=12, then what is the value of y -x ?
Text Solution
|
- A state college has separate fee retes for resident students and nonre...
Text Solution
|
- A sofa costs $50 less than three times the cost of a shair. If the sof...
Text Solution
|
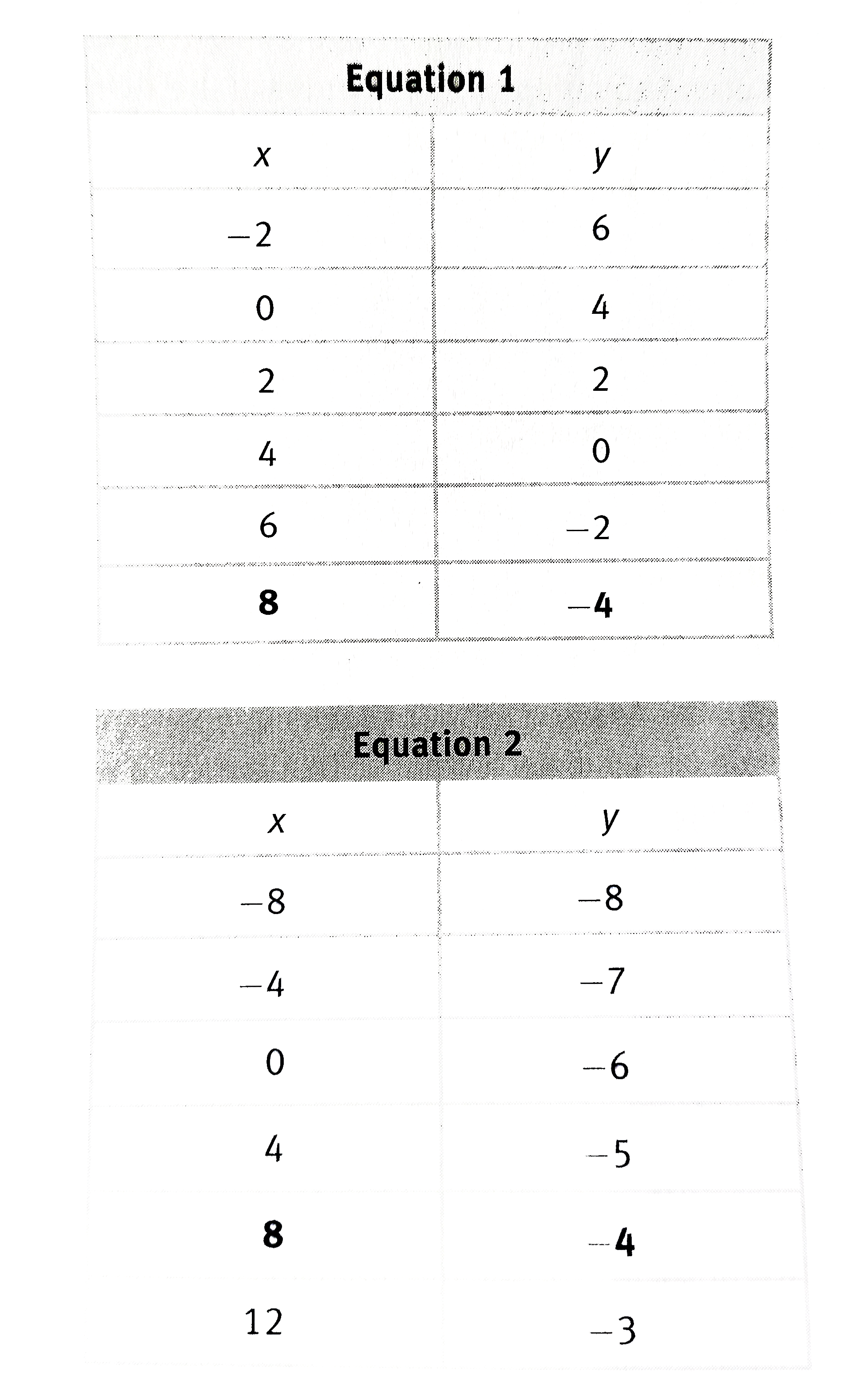
- The tables above represent data points for two linear equations. If th...
Text Solution
|
- If (A,B) is the solution to the system of equations shown above, and A...
Text Solution
|
- {{:(-16=7y+4x),(k = (7)/(8)y + (1)/(2)x ):} If the system of linear ...
Text Solution
|
- {{:(-13=ay+24x),(9+6bx=5y):} If the system of equations above has n...
Text Solution
|
- If 1/4x +2y = 11/4 and -6y -x=7, what is half
Text Solution
|
- At a certain toy store, tiny stuffed pandas cost $3.50 and giant stuff...
Text Solution
|
- A bead shop sell wooden beads for $0.20 each and crystal beads for $0....
Text Solution
|