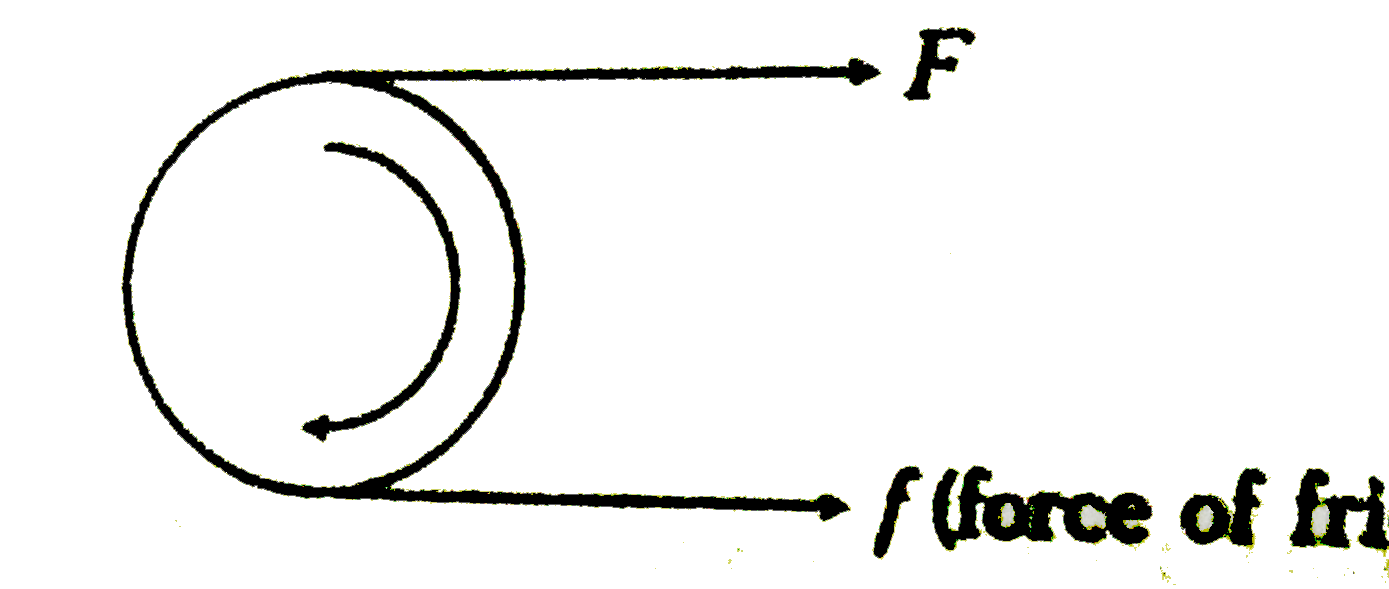Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY-ROTATION-(C) Chapter Exercises
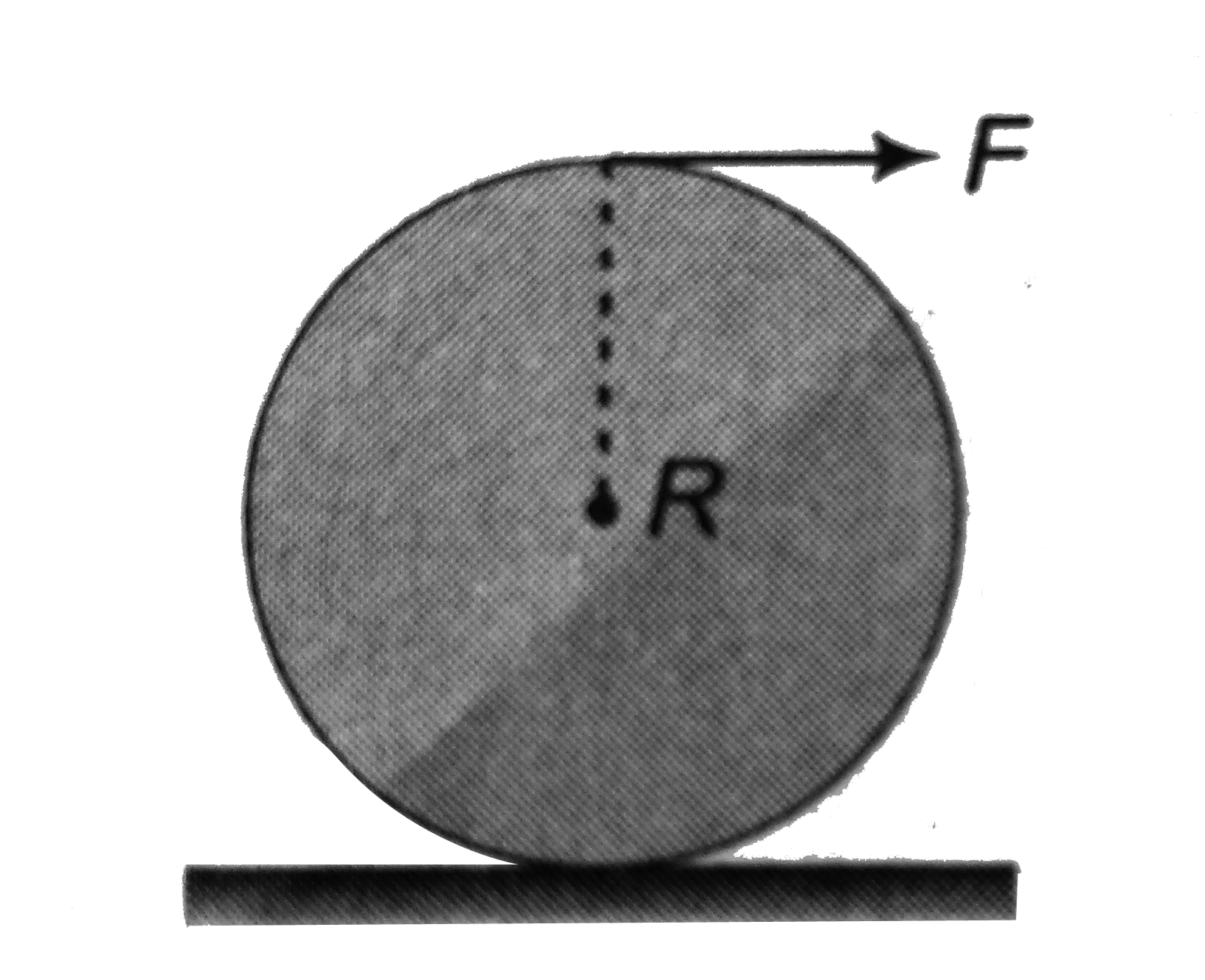
- A tangential force F acts at the top of a thin spherical shell of mass...
Text Solution
|
- A wheel of radius 10 cm can rotate freely about its centre as shown in...
Text Solution
|
- From a disc of radius R and mass M, a circular hole of diameter R, who...
Text Solution
|
- A disc and a solid sphere of same radius but different masses roll off...
Text Solution
|
- A uniform circular disc of radius 50 cm at rest is free to turn about ...
Text Solution
|
- A mass m moves in a circles on a smooth horizontal plane with velocity...
Text Solution
|
- Three identical spherical shells each of mass m and radius r are place...
Text Solution
|
- A uniform metallic rod rotates about its perpendicular bisector with ...
Text Solution
|
- A massless rod S having length 2l has equal point masses attached to i...
Text Solution
|
- A particle travels in a circle of radius 20 cm at a uniformly increasi...
Text Solution
|
- A solid sphere of radius r r is rolling on a horizontal surface. The r...
Text Solution
|
- If two circular discs A and B are of same mass but of radii r and 2r r...
Text Solution
|
- Choose the wrong statement.
Text Solution
|
- Two particle A and B are moving as shown in the figure Their tota...
Text Solution
|
- A rod of mass 5 kg is connected to the string at point B. The span of ...
Text Solution
|
- A particle moves with a constant velocity parallel to the X-axis. Its ...
Text Solution
|
- A ring of radius 0.5 m and mass 10 kg is rotating about its diameter w...
Text Solution
|
- A uniform sphere of mass 500 g rolls without slipping on a plane surfa...
Text Solution
|
- A rotating wheel changes angular speed from 1800 rpm to 3000 rpm in 20...
Text Solution
|
- The moment of inertia of ring about an axis passing through its diamet...
Text Solution
|
- Two bodies have their moments of inertia I and 2I, respectively about ...
Text Solution
|