Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTRIC CHARGES AND FIELDS
SUBHASH PUBLICATION|Exercise NUMERICALS WITH SOLUTIONS|21 VideosELECTRIC CHARGES AND FIELDS
SUBHASH PUBLICATION|Exercise THREE MARKS QUESTIONS WITH ANSWERS|12 VideosDUAL NATURE OF RADIATION AND MATTER
SUBHASH PUBLICATION|Exercise NUMERICALS WITH SOLUTIONS|21 VideosELECTROMAGNETIC INDUCTION
SUBHASH PUBLICATION|Exercise NUMERICALS WITH SOLUTIONS|19 Videos
Similar Questions
Explore conceptually related problems
SUBHASH PUBLICATION-ELECTRIC CHARGES AND FIELDS-FIVE MARKS QUESTIONS WITH ANSWERS
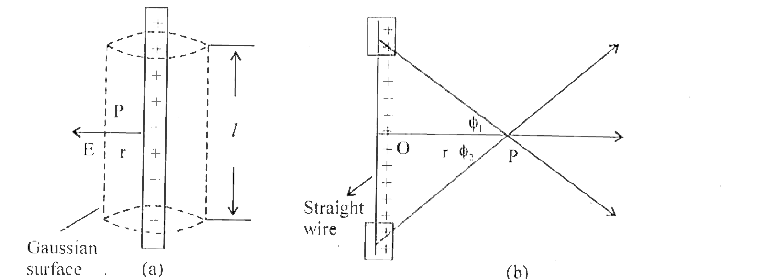
- State Gauss's theorem. Obtain an expression for elactric field at any ...
Text Solution
|
- Mention and five properties of electric field lines.
Text Solution
|
- Write the expression for torque experienced by an electric dipole in a...
Text Solution
|
- Given the expression for electric field intensity at a point due to a ...
Text Solution
|
- Write the expression for electric field at a point on the axis of a sh...
Text Solution
|
- Obtain an expression for the electric field intenstiy at a point on th...
Text Solution
|
- Give the expression for electric field intensity due to an infinite th...
Text Solution
|