Text Solution
Verified by Experts
Topper's Solved these Questions
GRAVITATION
MOTION|Exercise Exercise - 1 (Objective Problems | Jee Main|25 VideosGRAVITATION
MOTION|Exercise Exercise - 2 (Level - I) (Objective Problems | Jee Main|13 VideosGEOMETRICAL OPTICS
MOTION|Exercise Exercise - 4 | Level-II|55 VideosHEAT - 1
MOTION|Exercise EXERCISE -4 (Level - II) Previous Year | JEE Advanced|22 Videos
Similar Questions
Explore conceptually related problems
MOTION-GRAVITATION-Exercise - 4 Section - B Previous Years Problems
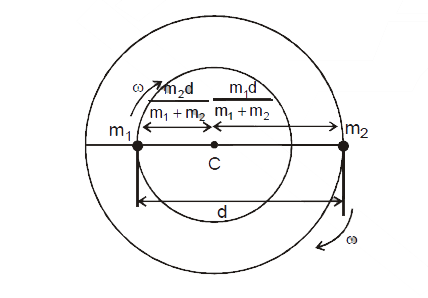
- In a double star, two stars (one of mass m and the other of mass 2m) d...
Text Solution
|
- Suppose the gravitational force varies inversely as the nth power of d...
Text Solution
|
- Average density of the earth
Text Solution
|
- The change in the value of g at a height h above the surface of the ea...
Text Solution
|
- A particle of mass 10g is kept on the surface of a uniform sphere of m...
Text Solution
|
- If gE and gM are the acceleration due to gravity on the surfaces of th...
Text Solution
|
- A planet in a distant solar systyem is 10 times more massive than the ...
Text Solution
|
- The height at which the acceleration due to gravity becomes (g)/(9) (w...
Text Solution
|
- Two bodies of masses m and 4m are placed at a distance r. The gravitat...
Text Solution
|
- Two particles of equal mass m go around a circle of radius R under act...
Text Solution
|
- The mass of a spaceship is 1000kg. It is to be launched from the earth...
Text Solution
|
- What is the minimum energy required to launch a satellite of mass m fr...
Text Solution
|
- Four particles, each of mass M and equidistant from each other, move a...
Text Solution
|
- From a solid sphere of mass M and radius R, a spherical portion of rad...
Text Solution
|
- A satellite is revolving in a circular orbit at a height 'h' from the ...
Text Solution
|
- The dependence of acceleration due to gravity g on the distance r from...
Text Solution
|