A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
MOTION|Exercise QUESTIONS FOR PRACTICE |38 VideosGRAVITATION
MOTION|Exercise Exercise - 1 (Section - A :- Newtons Law of Gravitation & Gravitational Field, Potential and Potential Energy) |28 VideosGRAVITATION
MOTION|Exercise Exercise - 4 | Level - I (Previous year | JEE Main)|16 VideosGEOMETRICAL OPTICS
MOTION|Exercise Exercise - 4 | Level-II|55 VideosHEAT - 1
MOTION|Exercise EXERCISE -4 (Level - II) Previous Year | JEE Advanced|22 Videos
Similar Questions
Explore conceptually related problems
MOTION-GRAVITATION-Exercise - 4 | Level - II (Previous Year | JEE Advanced)
- A system of binary stars of mass m(A) and m(B) are moving in circular ...
Text Solution
|
- Column I describes some situations in which a small object moves. Colu...
Text Solution
|
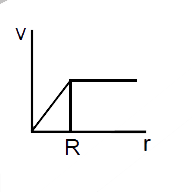
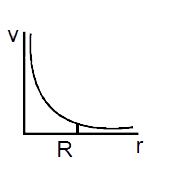
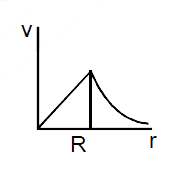
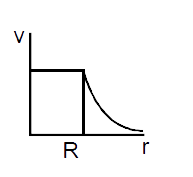
- A spherically symmetric gravitational system of particles has a mass d...
Text Solution
|
- Assertion : An astronaut in an orbiting space station above the earth ...
Text Solution
|
- A thin uniform disc (see figure) of mass M has outer radius 4R and in...
Text Solution
|
- A binary star consists of two stars A(mass 2.2 Ms) and B (mass 11 Ms)...
Text Solution
|
- Graviational acceleration on the surface of plane fo (sqrt6)/(11)g. wh...
Text Solution
|
- A satellite is moving with a constant speed 'V' in a circular orbit ab...
Text Solution
|
- Two spherical planets P and Q have the same uniform density rho, masse...
Text Solution
|
- Two bodies, each of mass M, are kept fixed with a separation 2L. A par...
Text Solution
|
- A planet of radius R=(1)/(10)xx(radius of Earth) has the same mass den...
Text Solution
|
- A larger spherical mass M is fixed at one position and two identical p...
Text Solution
|
- A bullet is fired vertically upwards with a velocity upsilon from the ...
Text Solution
|
- A planet of mass M, has two natural satellites with masses m1 and m2. ...
Text Solution
|
- Consider a spherical gaseous cloud of mass density rho(r) in a free sp...
Text Solution
|