Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
SUBHASH PUBLICATION-LINES AND ANGLES -EXERCISE 3.3
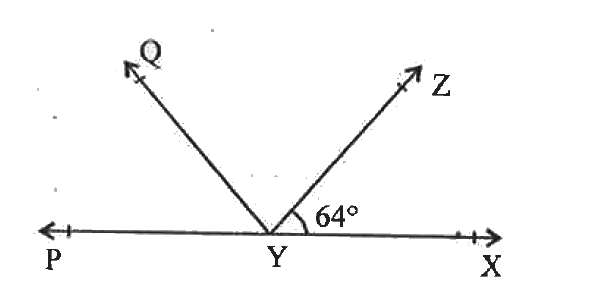
- It is given that lfloorXYZ = 64^(@) and XY is produced to point P. Dra...
Text Solution
|
- In Fig , sides QP and RQ and RQ of DeltaPQR are produced to points S a...
Text Solution
|
- In the Figure lfloorX = 62^(@),lfloorXYZ=54^(@). If YO and ZO are the ...
Text Solution
|
- In the Fig , if AB||DE, lfloorBAC=35^(@) and lfloorCDE=53^(@) , " find...
Text Solution
|
- In Fig , if lines PQ and RS intersect at point T, such that lfloorPRT=...
Text Solution
|
- In the Fig , if PQbotPS, PQ || SR,lfloorSQR = 28^(@) and lfloorQRT = ...
Text Solution
|
- In Fig , the side QR and DeltaPQR is produced to a point S. If the bis...
Text Solution
|