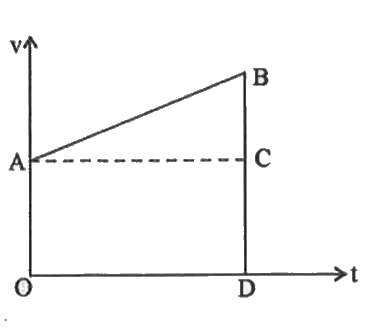
Let `'v_(0)'` be the initial velocity of a particle. Let 'a' be the uniform acceleration v - t graph gives a straight line with a constant slope, `tan theta=m`
`"i.e. "a=(v-v_(0))/(t)" ….(1)"`
From the figure OABD is a trapezium
Area of trapezium PABD = Area of rectangle OACD + Area of triangle ACB
The second term on the right indicates the additional distance covered by the particle due to acceleartion.
i.e. are of trapezium `=(OA)(OD)+1//2(AC)(BC)=v_(0)t+1//2t(v-v_(0))` by using (1)
Area of trapezium `=v_(0)t+1//2at^(2)`
From the dimensional analysis, the right hand terms indicate the distance travelled. From the principle of homogeneity , the left hand side term should indicate the distance covered.
Hence area of the trapezium `=x=v_(0)t+1//2at^(2)`
For a unform motion `a =0 and x=v_(0)t`
For a particle starting from rest `v_(0)=0, x=1//2 at^(2)`
In a vactor form, `vecx=vecv_(0)t+(1)/(2)veca t^(2)`
Note : For a vertical upward motion, `y=v_(0)t-(1)/(2)g t^(2)` and for a vertical downward motion and `-y=-v_(0)t-(1)/(2) g t^(2)," i.e., "y=v_(0)t+(1)/(2)g t^(2)`.
