Text Solution
Verified by Experts
Topper's Solved these Questions
FORCE AND NEWTONS LAWS OF MOTION
GRB PUBLICATION|Exercise Problem for practice|30 VideosFORCE AND NEWTONS LAWS OF MOTION
GRB PUBLICATION|Exercise Objective Questions|134 VideosFORCE AND NEWTONS LAWS OF MOTION
GRB PUBLICATION|Exercise Comprehension|12 VideosBASIC MATHEMATICS
GRB PUBLICATION|Exercise Problems For Practice|35 VideosFRICTION AND CIRCULAR MOTION
GRB PUBLICATION|Exercise Comprehension type|11 Videos
Similar Questions
Explore conceptually related problems
GRB PUBLICATION-FORCE AND NEWTONS LAWS OF MOTION-Problem
- What is the tension in a rod of length length L and mass M at a dista...
Text Solution
|
- A small mirror of area A and mass m is suspended in a vertical plane b...
Text Solution
|
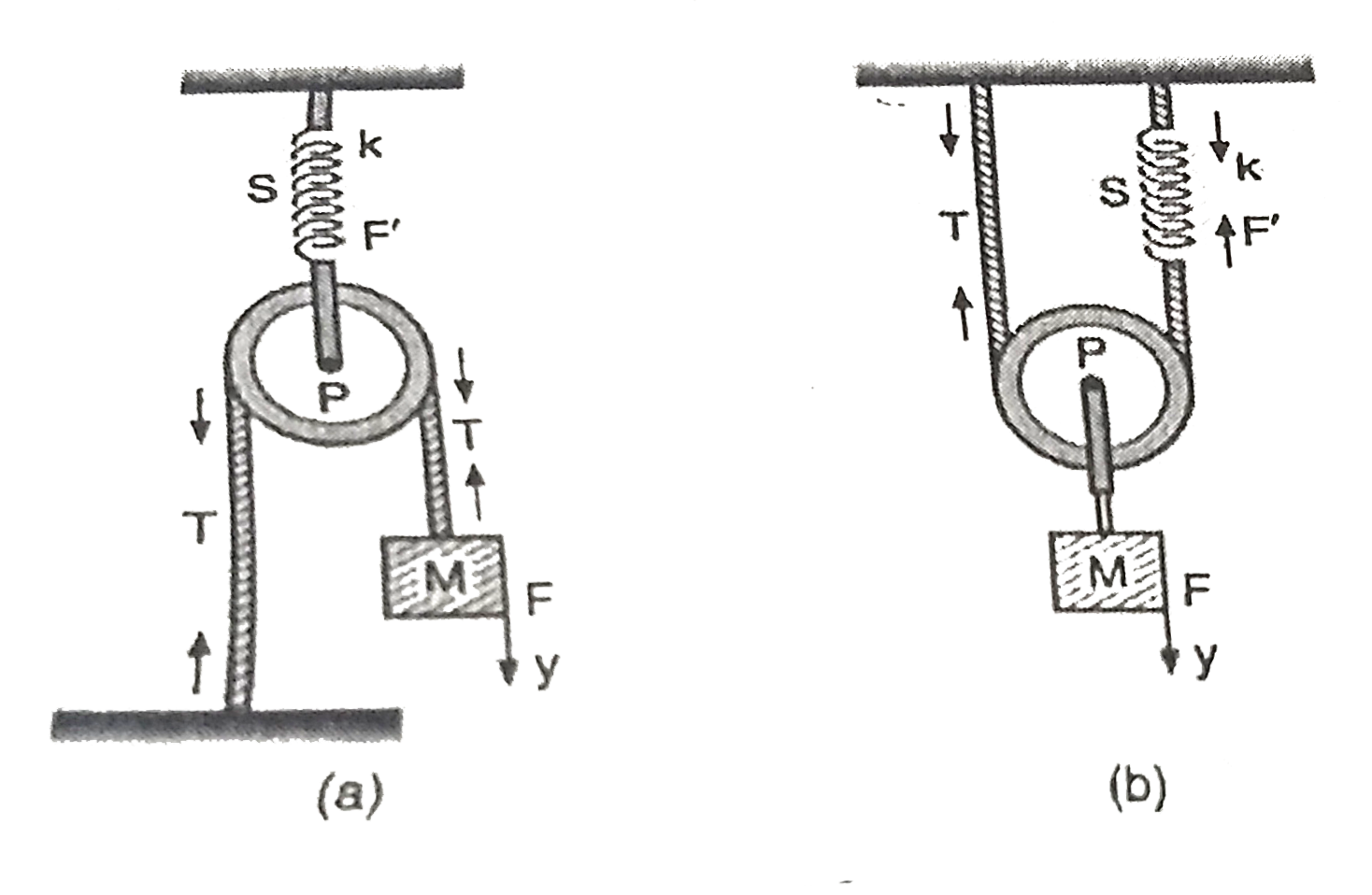
- The pulley arrangements of Figs. (a) and (b) are identical. The mass o...
Text Solution
|
- Three equal weights of mass m each are hanging on a string passing ove...
Text Solution
|
- An elevator and its load weigh a total of 166 kg. Find the tension T i...
Text Solution
|
- In the situation shown in figure, both the pulleys and the strings are...
Text Solution
|
- A monkey of mass m climbs up to a rope hung over a fixed pulley. The o...
Text Solution
|
- Two 100 g blocks hang at the ends of a light flexible cord passing ove...
Text Solution
|
- A dynomometer D (a force meter ) is attached to two masses M = 10 kg a...
Text Solution
|
- A disc of mass m(2) is placed on a table. A stiff spring is attached t...
Text Solution
|
- Two blocks A and B are connected to each other by a string and a sprin...
Text Solution
|
- On applying a force F the mass M is displaced vertically down by from ...
Text Solution
|
- What are the rate of change of momenta of the pendulum bobs 1 and 2 as...
Text Solution
|
- At wood machine is attached below the left hand pan of a physical bala...
Text Solution
|
- Find the mass of the hanging block in which will prevent the smaller b...
Text Solution
|
- In the figure a painter of mass 100 kg pulls himself up with the crate...
Text Solution
|
- A very flexible uniform chain of mass M and length L is suspended vert...
Text Solution
|
- One end (say B) of a massless spring having force constant k is attach...
Text Solution
|
- In the pulley system shown the movable pulleys A,B and C have mass m e...
Text Solution
|
- Write equations of forces in terms of the relative acceleration for th...
Text Solution
|