A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
FORCE AND NEWTONS LAWS OF MOTION
GRB PUBLICATION|Exercise More than one choice is correct|15 VideosFORCE AND NEWTONS LAWS OF MOTION
GRB PUBLICATION|Exercise Assertion- Reason|4 VideosFORCE AND NEWTONS LAWS OF MOTION
GRB PUBLICATION|Exercise Problem for practice|30 VideosBASIC MATHEMATICS
GRB PUBLICATION|Exercise Problems For Practice|35 VideosFRICTION AND CIRCULAR MOTION
GRB PUBLICATION|Exercise Comprehension type|11 Videos
Similar Questions
Explore conceptually related problems
GRB PUBLICATION-FORCE AND NEWTONS LAWS OF MOTION-Objective Questions
- A machine gun fires a bullet of mass 40 gm with a speed 1200 m//s The ...
Text Solution
|
- The upper half of an inclined plane with inclination phi is perfectly ...
Text Solution
|
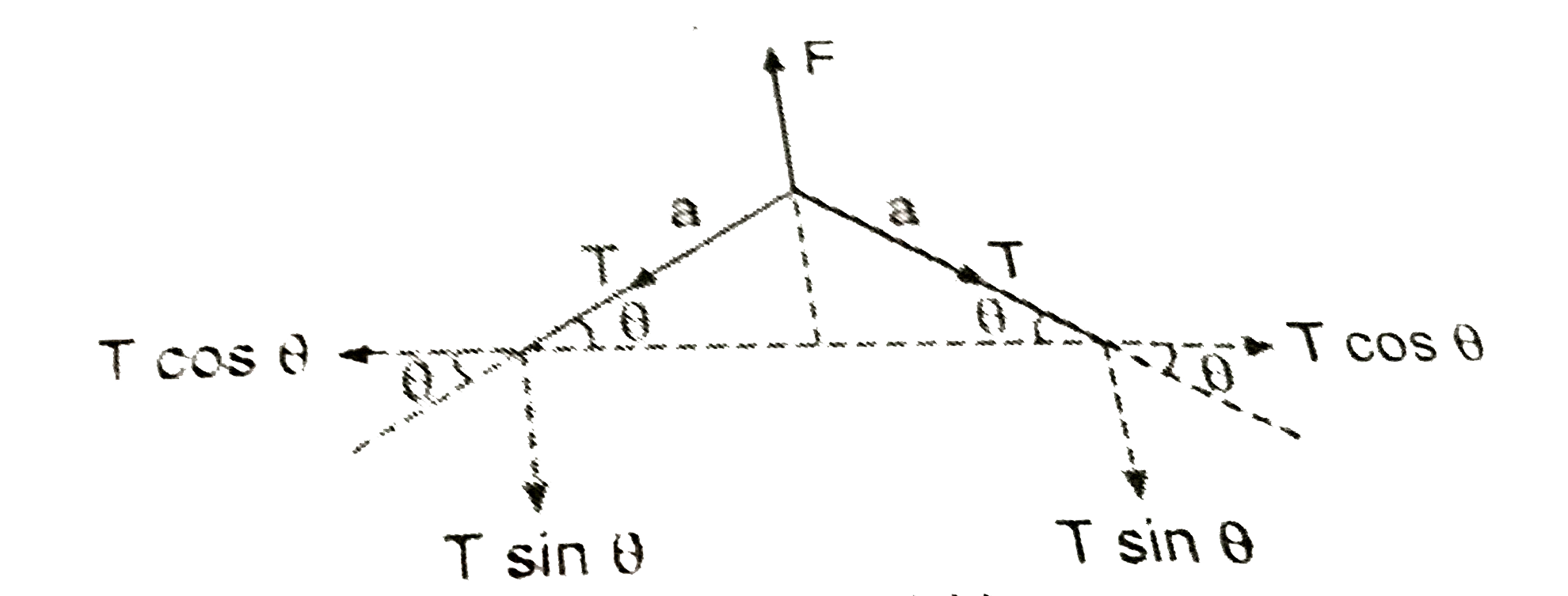
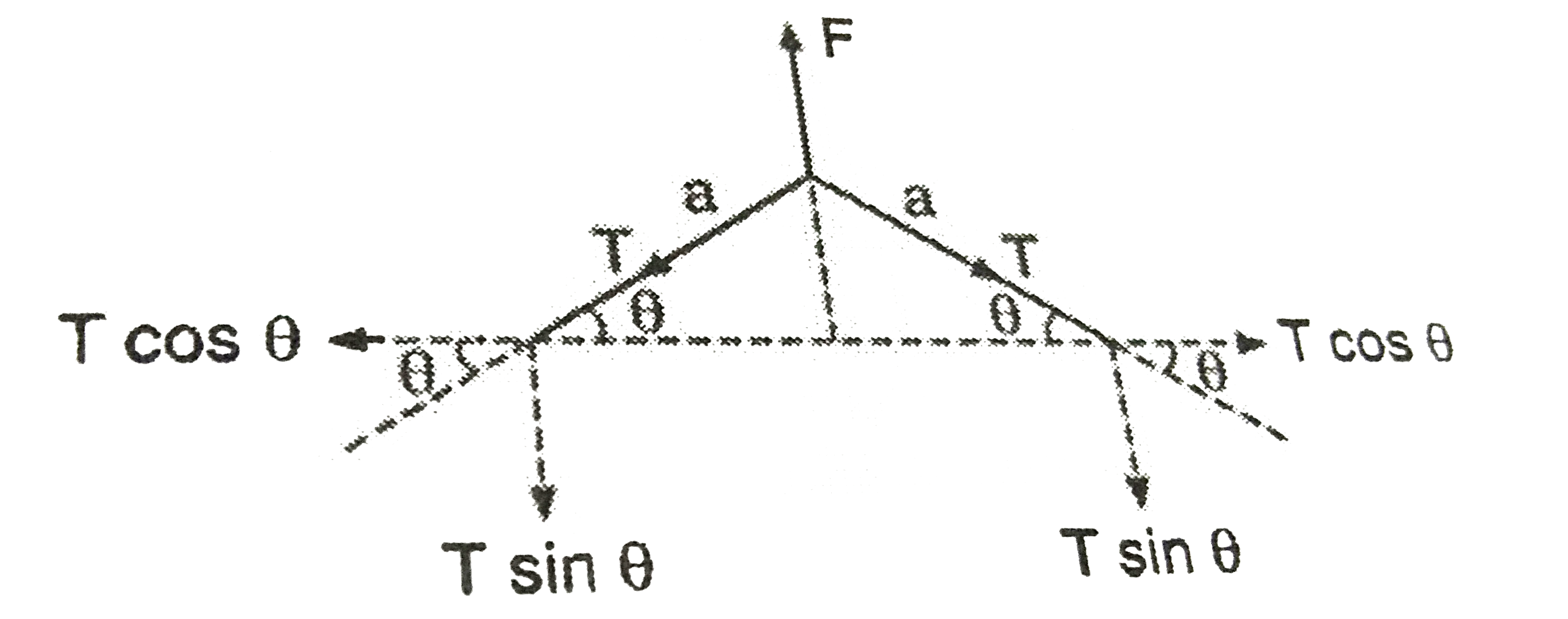
- Two particles of mass 'm' each are tied at eh ends of a light string o...
Text Solution
|
- A particle moves in the x-y plane under is influence of a force such t...
Text Solution
|
- A balloon of gross weight W newton descends with an acceleration fm//s...
Text Solution
|
- A load W is to be raised by a rope from rest to rest through a height ...
Text Solution
|
- Two steel balls A and B are placed inside a right circular cylinder of...
Text Solution
|
- Two persons of equal weight are hanging by their hands from the ends o...
Text Solution
|
- In the diagram given below all surfaces are frictionless. What horizon...
Text Solution
|
- If the above diagram initially there is no elongation in spring if the...
Text Solution
|
- A player caught a criket ball of mass 150 g moving at the rate of 20 m...
Text Solution
|
- A block of mass 'm' is connected to another block of mass 'M' by a spr...
Text Solution
|
- A boy is hanging from a horizontal branch of a tree. The tension in th...
Text Solution
|
- A bullet of mass 0.05 kg moving with a speed of 80m//s enters a wooden...
Text Solution
|
- Two blocks 4 kg and 2 kg are sliding down an incline plane as shown in...
Text Solution
|
- Sand is being dropped on a conveyor belt at the rate of Mkg//s . The f...
Text Solution
|
- A steel wire can withstand a load up to 2940N. A load of 150 kg is sus...
Text Solution
|
- A mass of 10 kg is suspended from a spring balance, it is pulled aside...
Text Solution
|
- Three concurrent co-planer force 1N , 2N and 3N acting along different...
Text Solution
|
- A mass of 1 kg is just able to slide down the slope of an inclined rou...
Text Solution
|