Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT-MECHANICAL PROPERTIES OF SOLIDS-EXERCISE
- Fig., shows the stress-strain curve for a given materal. What are (a) ...
Text Solution
|
- The stress versus strain graph for two materials A and B are shown in ...
Text Solution
|
- Read each of the statement below carefully and state, with reasons, if...
Text Solution
|
- Two wires of diameter 0.25 cm, one made of steel and the other made of...
Text Solution
|
- The edges of an aluminum cube are 10 cm long. One face of the cube is ...
Text Solution
|
- Four identical hollow cylindrical cloumns of steel support a big struc...
Text Solution
|
- A piece of copper having a rectangular cross section of 15.2 xx 19.1 m...
Text Solution
|
- A steel cable with a radius of 1.5 cm support a chairlift at a ski are...
Text Solution
|
- A rigid bar of mass 15 kg is supported symmetrically by three wires ea...
Text Solution
|
- A 14.5 kg mass, fastened to the end of a steel wire of unstretched len...
Text Solution
|
- Compute the bulk modulus of water from the following data : initial vo...
Text Solution
|
- What is the density of ocean water at a depth, where the pressure is 8...
Text Solution
|
- Compute the fractional change in volume of a glass slab, when subjecte...
Text Solution
|
- Determine the volume contraction of a solid copper cube, 10 cm on an e...
Text Solution
|
- How much should the pressure on a litre of water be changed to compres...
Text Solution
|
- Anvils made of single crystal of diamond , with shape as shown in fig....
Text Solution
|
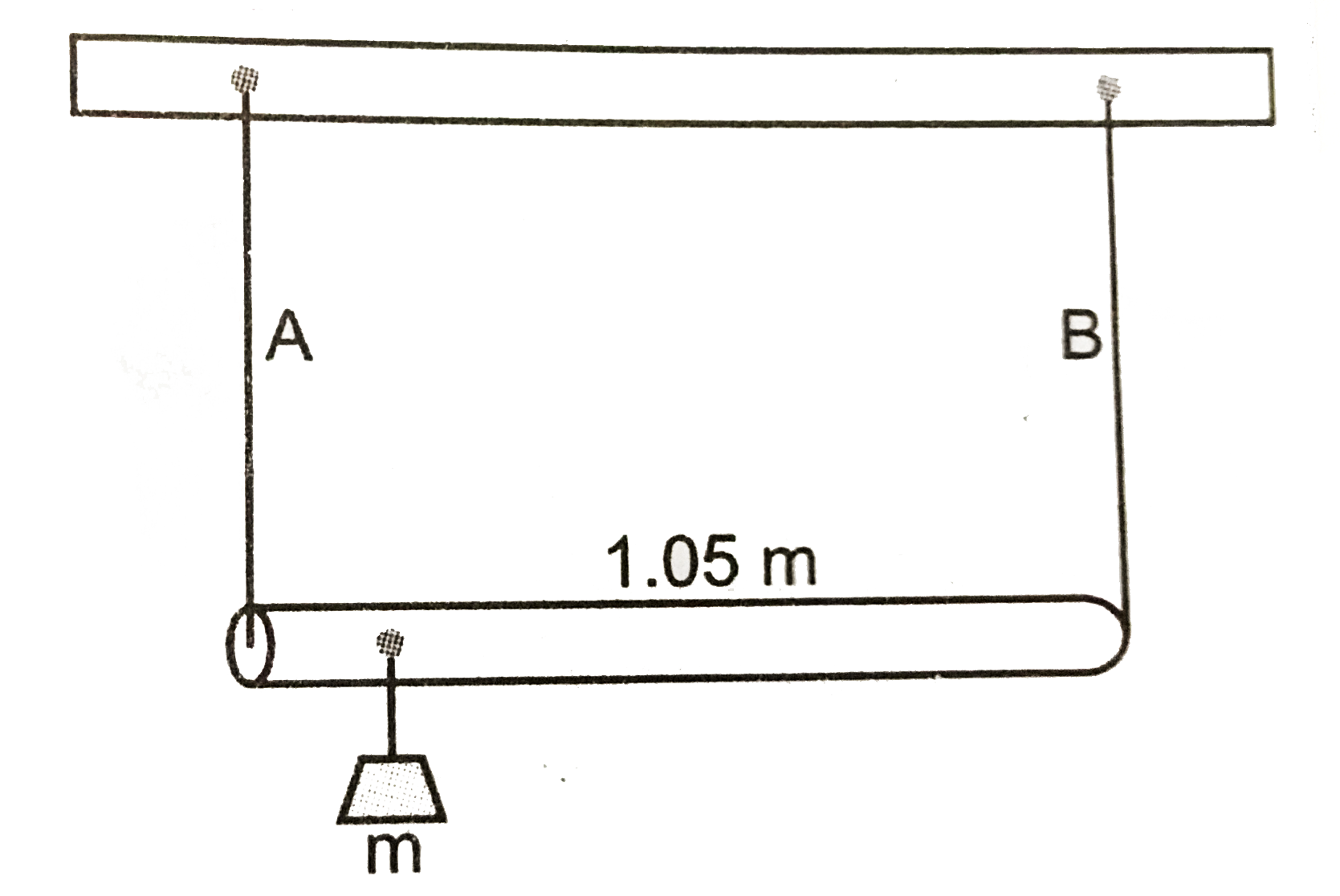
- A rod of length 1.05 m having negliaible mass is supported at its ends...
Text Solution
|
- A mild steel wire of length 1.0 m and cross-sectional are 0.5 xx 10^(-...
Text Solution
|
- Two strips of metal are riveted together at their ends by four rivets,...
Text Solution
|
- The marina Trench is located in the pacific ocean, and at one place it...
Text Solution
|