Home
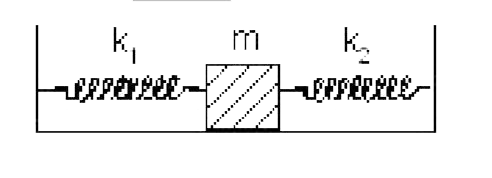
Class 12
PHYSICS
A block of mass m is connected between t...

A block of mass m is connected between two springs (constants `K_(1)` and `K_(2) )` as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-

A

`(1)/(2pi) ((m)/(K_(1)+K_(2)))^(1//2)`

B

`(1)/(2pi) ((K_(1)K_(2))/((K_(1)+K_(2))m))^(1//2)`

C

`(1)/(2pi) ((K_(1)+K_(2))/(m))^(1//2)`

D

`(1)/(2pi) (((K_(1)+K_(2))m)/(K_(1)K_(2)))^(1//2)`

Text Solution

Verified by Experts

The correct Answer is:
C
Promotional Banner

Topper's Solved these Questions

  • SIMPLE HARONIC MOTION

    MOTION|Exercise EXERCISE -1 ( SECTION-E,F ) ( – Angu lar shm & s implependulum)|10 Videos

  • SIMPLE HARONIC MOTION

    MOTION|Exercise EXERCISE -1 ( SECTION - G ) ( Compound pendulum / physical pendulum, torsional pendulum|5 Videos

  • SIMPLE HARONIC MOTION

    MOTION|Exercise EXERCISE -1 ( SECTION-C ) ( Two block system)|6 Videos

  • SIMPLE HARMONIC MOTION

    MOTION|Exercise EXERCISE -3 Section - B Previous Year Problems | JEE MAIN|23 Videos

  • SOUND WAVES

    MOTION|Exercise Exercise - 3 (Section - B)|14 Videos

Similar Questions

Explore conceptually related problems

Two spring of spring constants k_(1) and k_(2) ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

The frequency of oscillation of the spring shown in the figure will be

A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?

The frequency of oscillation of the springs shown in the figure will be

A rod of mass m and length l is connected by two spring of spring constants k_(1) and k_(2) , so that it is horizontal at equilibrium. What is the natural frequency of the system?

A block is placed on a frictionless horizontal table. The mass of the block is m and springs are attached on either side with force constants K_(1) and K_(2) . If the block is displaced a little and left to oscillate, then the angular frequency of oscillation will be

A block of mass M is placed on a smooth table. Its two sides are attached to the fixed walls by means of collinear horizontal springs of spring constants K_(1) and K_(2) respectively (K_(1) gt K_(2)) as shown in the figure. The block is made to oscillate horizontally along the line of two springs. The frequency of its oscillation is