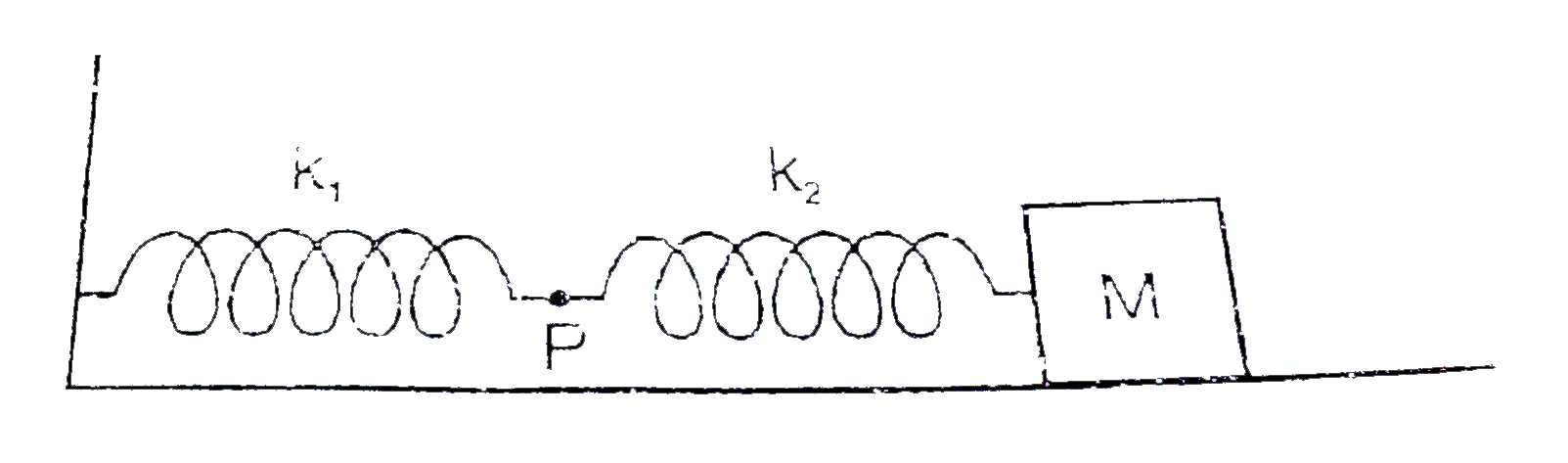A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SIMPLE HARONIC MOTION
MOTION|Exercise EXERCISE -4 (Leve-II) [ JEE 2011]|11 VideosSIMPLE HARONIC MOTION
MOTION|Exercise EXERCISE -4 (Leve-I)|23 VideosSIMPLE HARMONIC MOTION
MOTION|Exercise EXERCISE -3 Section - B Previous Year Problems | JEE MAIN|23 VideosSOUND WAVES
MOTION|Exercise Exercise - 3 (Section - B)|14 Videos
Similar Questions
Explore conceptually related problems
MOTION-SIMPLE HARONIC MOTION -EXERCISE -4 (Leve-II)
- A simple pendulum has time period (T1). The point of suspension is now...
Text Solution
|
- A mass m is undergoing SHM in the verticl direction about the mean pos...
Text Solution
|
- The function x = A sin^2 (omega)t + B cos^2 (omega)t + Csin (omega)t c...
Text Solution
|
- A block (B) is attached to two unstriched sprig S(1) and S(2) with spr...
Text Solution
|
- The x-t graph of a particle undergoing simple harmonic motion is shown...
Text Solution
|
- The mass M shown in the figure oscillates in simple harmnonic motion a...
Text Solution
|
- A uniform rod of length L and mass M is pivotedat the centre. Its two ...
Text Solution
|
- A metal rod of length 'L' and mass 'm' is piovted at one end. A thin d...
Text Solution
|