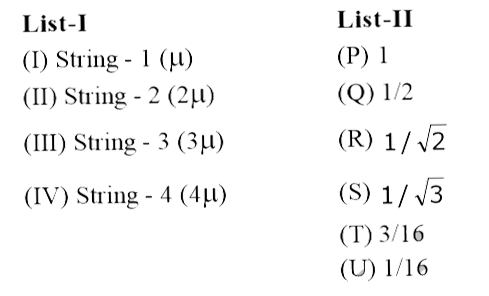A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MOTION-WAVES-EXERCISE -4 (Level -II) (previous year JEE Advanced)
- A transverse harmonic disturbance is produced in a string. The maximum...
Text Solution
|
- A massless rod is suspended by two identical strings AB and CD of equa...
Text Solution
|
- A transverse sinusoidal wave moves along a string in the positive x-di...
Text Solution
|
- A 20 cm long string, having a mass of 1.0 g, is fixed at both the ends...
Text Solution
|
- When two progressive waves y(1) = 4 sin (2x - 6t) and y(2) = 3 sin (2x...
Text Solution
|
- A horizontal stretched string, fixed at two ends, is vibrating in its ...
Text Solution
|
- One end of a taut string of length 3m along the x-axis is fixed at x =...
Text Solution
|
- Four harmonic waves of equal freuencies and equal intensity I(0) have ...
Text Solution
|
- A musical instrument is made using four different metal strings, 1, 2,...
Text Solution
|
- A musical instrument is made using four different metal strings, 1, 2,...
Text Solution
|