Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MOTION-ROTATIONAL MOTION -Exercise - 3 ( Section-B )
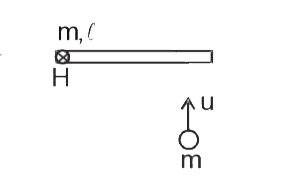
- A uniform rod of mass m and length l can rotate freely on a smooth h...
Text Solution
|
- A 'T' shaped object with dimensions shown in the figure, is lying on a...
Text Solution
|
- The moment of inertia of a uniform semicircular disc of mass M and rad...
Text Solution
|
- A thin circular ring of mass m and radius R is rotating about its axis...
Text Solution
|
- Four point masses, each of value m, are placed at the corners of a squ...
Text Solution
|
- A coin is placed on a horizontal platform which undergoes vertical sim...
Text Solution
|
- A force of - F hat k on O, the origin of the coordinate system. The to...
Text Solution
|
- Angular momentum of the particle rotating with a central force is con...
Text Solution
|
- A round uniform body of radius R, mass M and moment of inertia 'I' rol...
Text Solution
|
- For the given uniform square lamina ABCD, whose centre is O
Text Solution
|
- A circular disc of radius R is removed from a bigger circular disc of ...
Text Solution
|
- Consider a uniform square plate of side 'a' and mass 'm'. The moment o...
Text Solution
|
- A thin uniform rod of length l and mass m is swinging freely about a h...
Text Solution
|
- A pulley os radius 2m is rotated about its axis by a force F= (20 t- ...
Text Solution
|
- A thin horizontal circular disc is roating about a vertical axis passi...
Text Solution
|
- A hoop of radius r and mass m rotating with an angular velocity omega0...
Text Solution
|
- A bob of mass m attached to an inextensible string of length I is susp...
Text Solution
|
- A mass 'm' is supported by a massless string wound around a uniform ho...
Text Solution
|
- A block of mass is placed on a surface with a vertical cross section g...
Text Solution
|
- From a solid sphere of M and radius R a cube of maximum possible volu...
Text Solution
|
- A roller is made by joining together two cones at their vertices O, ti...
Text Solution
|