Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
GRB PUBLICATION-VECTORS-INTERGER ANSWER
- A point moves according to the law" "x= at, y=at (1 -alphat) where a...
Text Solution
|
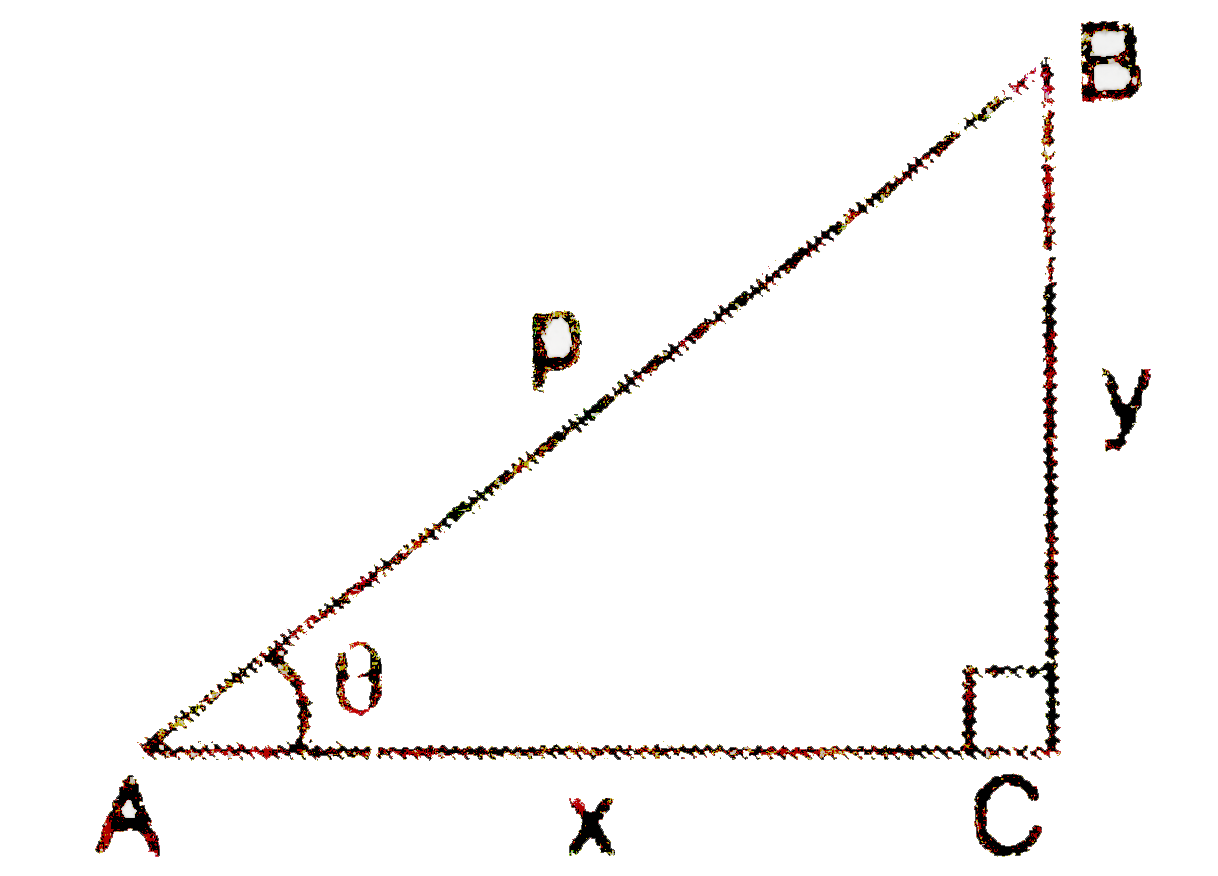
- If ABC is a right angled triangle with hypotenuse AB=P. Then vecAB....
Text Solution
|
- Two foreces vecP and vecQ are acting at a point . If vecP is reverse...
Text Solution
|
- Given vecr = A cos alphat hati + B sin alphat hatj. Then if (d^(2) ve...
Text Solution
|
- If vector A is perpendicular to vectors B and |vecA + vecB| =n|vecA +...
Text Solution
|
- If 0.8 hati + 0.2chatj represents direction, then the value of c will...
Text Solution
|
- If the angle between 2hati+ 2hatj- hatk and vector hati + chatk is a...
Text Solution
|
- |vecA + vecB|^(2) - |vecA - vecB|^(2) = n vecA. vecB The value of n...
Text Solution
|
- For the value of a, vecA = 2hati +a hatj +hatk is prependicular to v...
Text Solution
|