Six point masses of mass `m` each are at the vertices of a regular hexagon of side `l`. Calculate the force on any of the masses.

Explanation

Consider the diagram below, in which six point masses are placed at six vertices A, B, C, D, E and F

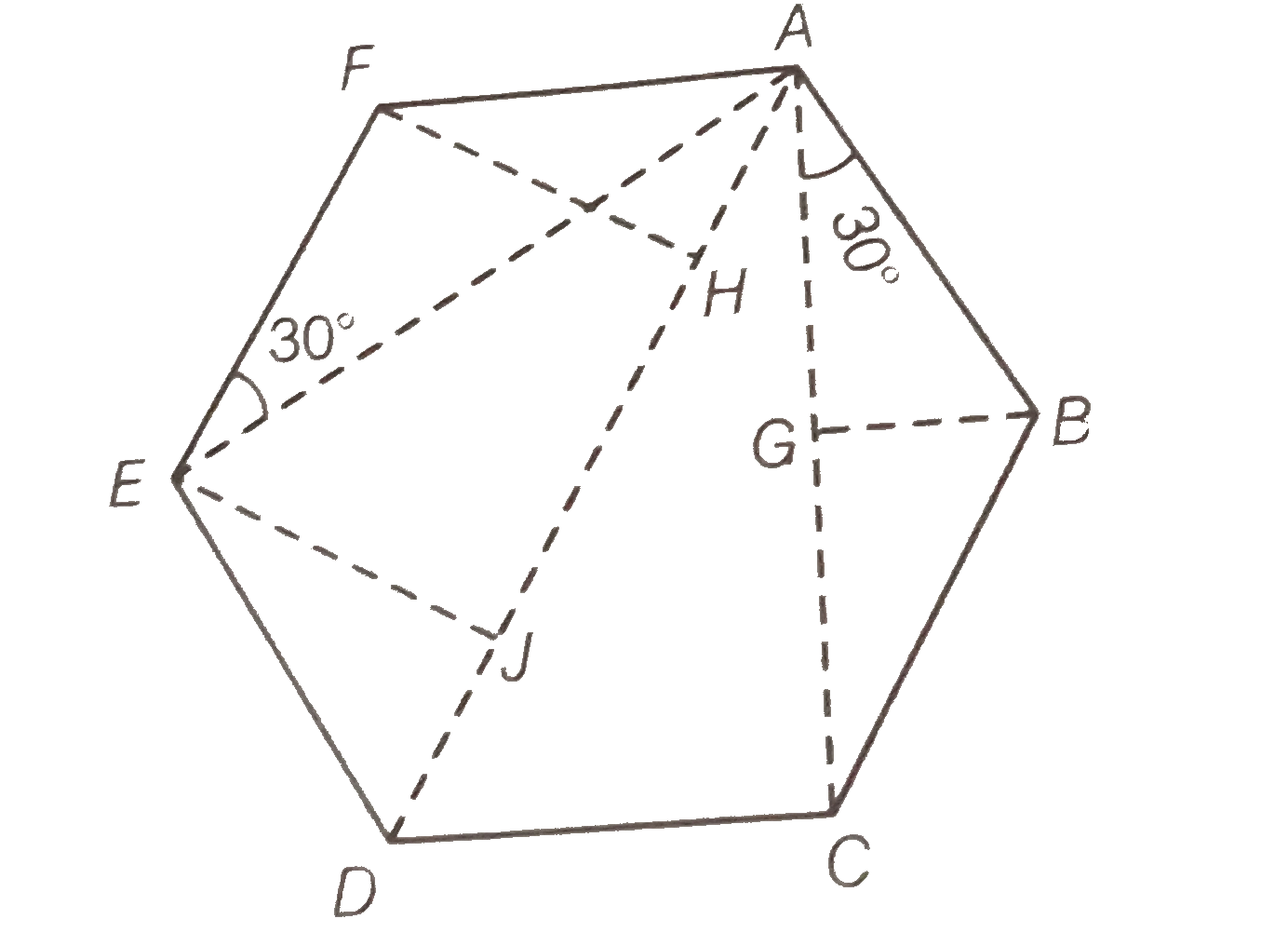
`AC = AG + GC = 2AG`
`= 2 l cos 30^(@) = 2l sqrt3//2`
`= sqrt3l = AE`
`AD = AH + HJ + JD`
`= l sin 30^(@) + l + l sin 30^(2) = 2l`
Force on mass m at A due to mass m at B is, `f_(1) = (Gmm)/(l^(2))` along AB.
Force on mass m at A due to mass m at C is, `f_(2) = (Gm xx m)/((sqrt(3l))^(2)) = (Gm^(2))/(3l^(2))` along AC. [`:. AC = sqrt(3l)`]
Force on mass m at A due to mass m at D is, `f_(3) = (Gm xx m)/((2l)^(2)) = (Gm^(2))/(4l^(2))` along AD `[ :. AD = 2l]`
Force on mass m at A due to mass m at E is `f_(4) = (Gm xx m)/((sqrt(3l))^(2)) = (Gm^(2))/(3l^(2))` along AE.
`f_(5) = (Gm xx m)/(l^(2)) = (Gm^(2))/(l^(2))` along AF.
Resultant force due to `f_(1)` and `f_(5)` is `F_(1) = sqrt(f_(1)^(2) + f_(5)^(2) + 2f_(1) f_(5) cos 120^(@)) = (Gm^(2))/(l^(2))` along AD.
[`:.` Angle between `f_(1)` and `f_(5) = 120^(@)`]
Resultant force due to `f_(2)` and `f_(4)` is, `F_(2) = sqrt(t_(2)^(2) + t_(4)^(2) + 2f_(2)f_(4) cos 60^(@))`
`= (sqrt3 Gm^(2))/(3l^(2)) = (Gm^(2))/(sqrt(3l^(2))` along AD.
So, net force along AD `= F_(1) + F_(2) + F_(3) = (Gm^(2))/(l^(2)) + (Gm^(2))/(sqrt(3l)^(2)) + (Gm^(2))/(4l^(2)) = (Gm^(2))/(l^(2)) (1+ (1)/(sqrt3) + (1)/(4))`