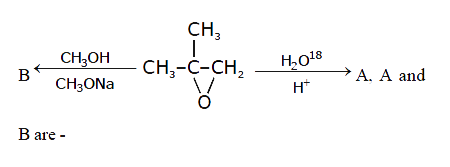A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ALCOHOLS & ETHERS
MOTION|Exercise EXERCISE -2 (LEVEL -II) MULTIPLE CORRECT JEE ADVANCED|21 VideosALCOHOLS & ETHERS
MOTION|Exercise EXERCISE -3 OBJECTIVE PROBLEMS JEE ADVANCED|17 VideosALCOHOLS & ETHERS
MOTION|Exercise EXERCISE -1 OBJECTIVE PROBLEMS JEE MAIN|47 VideosALKYI HALIDE
MOTION|Exercise Exercise - 4 | Level-II|8 Videos
Similar Questions
Explore conceptually related problems
MOTION-ALCOHOLS & ETHERS-EXERCISE -2 (LEVEL -I) OBJECTIVE PROBLEMS JEE MAIN
- A compound X with moleuclar formula C(3)H(8)O can be oxidized to a com...
Text Solution
|
- Glycerol overset(KHSO(4))to A overset(LiAlH(4))to B.
Text Solution
|
- A and B are
Text Solution
|
- Select schemes A, B, C out of - I. acid catalysed hydration II. ...
Text Solution
|
- CH3MrBr E is
Text Solution
|
- overset(Alc.KOH)to Major product is -
Text Solution
|
- A & B are
Text Solution
|
- CH2=CH underset(OH)underset(|)CHCH2CH2OH overset(MnO2)to A, A is
Text Solution
|
- What will be the chief productg from the following reaction sequence ?
Text Solution
|
- Which of the following reagents cannot be used for the oxidation of 1^...
Text Solution
|
- A water soluble C6H(14)O2 ompound is oxidized by lead tetraacetate (o...
Text Solution
|
- A racemic mixture of (+-) 2-pheynl propanoic acid on esterification wi...
Text Solution
|
- Which of the following alcohol can not be oxidized by KMnO4
Text Solution
|
- Which of the following is wrong -
Text Solution
|
- Which of the following reacts fastest with conc. HCl ?
Text Solution
|
- Compare the rate of acid catalyst dehydration
Text Solution
|
- Major product 'P' is :
Text Solution
|
- CH3-overset(CH3)overset(|)underset(CH3)underset(|)C-CH2CH2CH2OH overse...
Text Solution
|
- Identify the correct statement about reaction and products
Text Solution
|
- overset(H^(oplus))underset(Delta)to Major product Major product is
Text Solution
|