Home
Class 9
MATHS
AD is a diameter of a circle and AB is a...

AD is a diameter of a circle and AB is a chord. If AD = 34cm, AB = 30cm, the distance of AB form the centre of the circle is

A

`17` cm

B

`15` cm

C

`4` cm

D

`8` cm

Text Solution

Verified by Experts

The correct Answer is:
D
Given, AD = 34 cm and AB = 30 cm
In figure, draw `OLbotAB`.
Since, the perpendicular from the centre of a circle to a chord bisects the chord.

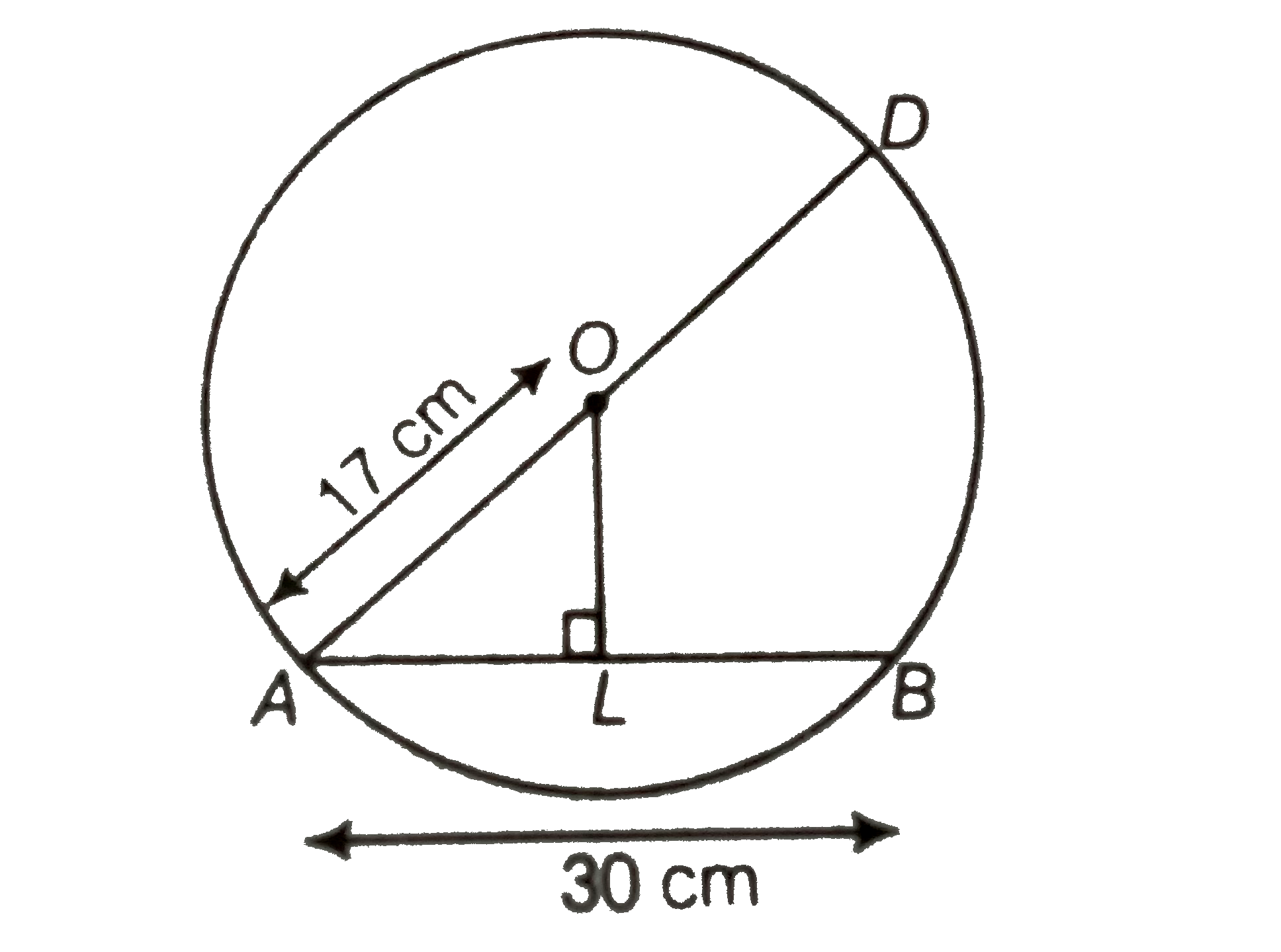
`:.AL=LB=1/2 AB=15cm`
`"In right angled "DeltaOLA, OA^(2)=OL^(2)+AL^(2) "[by pythagoras theorem]"`
`:.(17)^(2)=OL^(2)+(15)^(2)`
` Rightarrow289=OL^(2)+225`
`Rightarrow OL^(2)=289-225=64`
`:. OL=8 cm`
[taking positive square root, because length is always positive]
Hence, the distance of the chord from the centre is 8 cm.
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    NCERT EXEMPLAR|Exercise Exercise 10.4|2 Videos

  • Areas of Parallelograms and Triangles

    NCERT EXEMPLAR|Exercise Areas Of Parallelograms And Triangles|34 Videos

  • CONSTRUCTIONS

    NCERT EXEMPLAR|Exercise Long Answer Type Questions|5 Videos

Similar Questions

Explore conceptually related problems

AD is the diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is

In the adjoining figure, O is the centre of circle and diameter AC = 26 cm . If chord AB = 10 cm , then the distance between chord AB and centre O of the circle is :

In the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.

In the figure, seg AB is a chord of a circle with centre P. If PA = 8 cm and distance of chord AB from the centre P is 4 cm, find the area of the shaded portion.

AB is a chord of a circle with centre O and diameter 20 cm. If AB = 12 cm, find the distance of AB from O.

AB and CD are parallel chords of a circle 3 cm apart. If AB = 4 cm, CD = 10 cm, then what is the radius of the circle ?

O' is the centre of the circle, AB is a chord of the circle, OM_|_ AB . If AB= 20 cm, OM = 2sqrt(11) cm, then radius of the circle is

Radius of a circle is 34 cm and the distance of the chord from the centre is 30 cm, find the length of the chord .

A circle is drawn on AB as diameter. The centre of the circle is O and the length AB = 13 cm. P is a point on the circumference of the cirlces such that the chord AP = 12 cm. Calculate the value of the angles PAB and POB in radians :