Home
Class 9
MATHS
If the perpendicular bisector of a chord...

If the perpendicular bisector of a chord AB of a circle PXAQBY intersects the circle at P and Q, prove that arc `PXA cong"arc "PYB`.

Text Solution

Verified by Experts

Let AB be a chord of a circle having centre at OPQ be the perpendicular bisector of the chord AB, which intersects at M and it always passes through O.

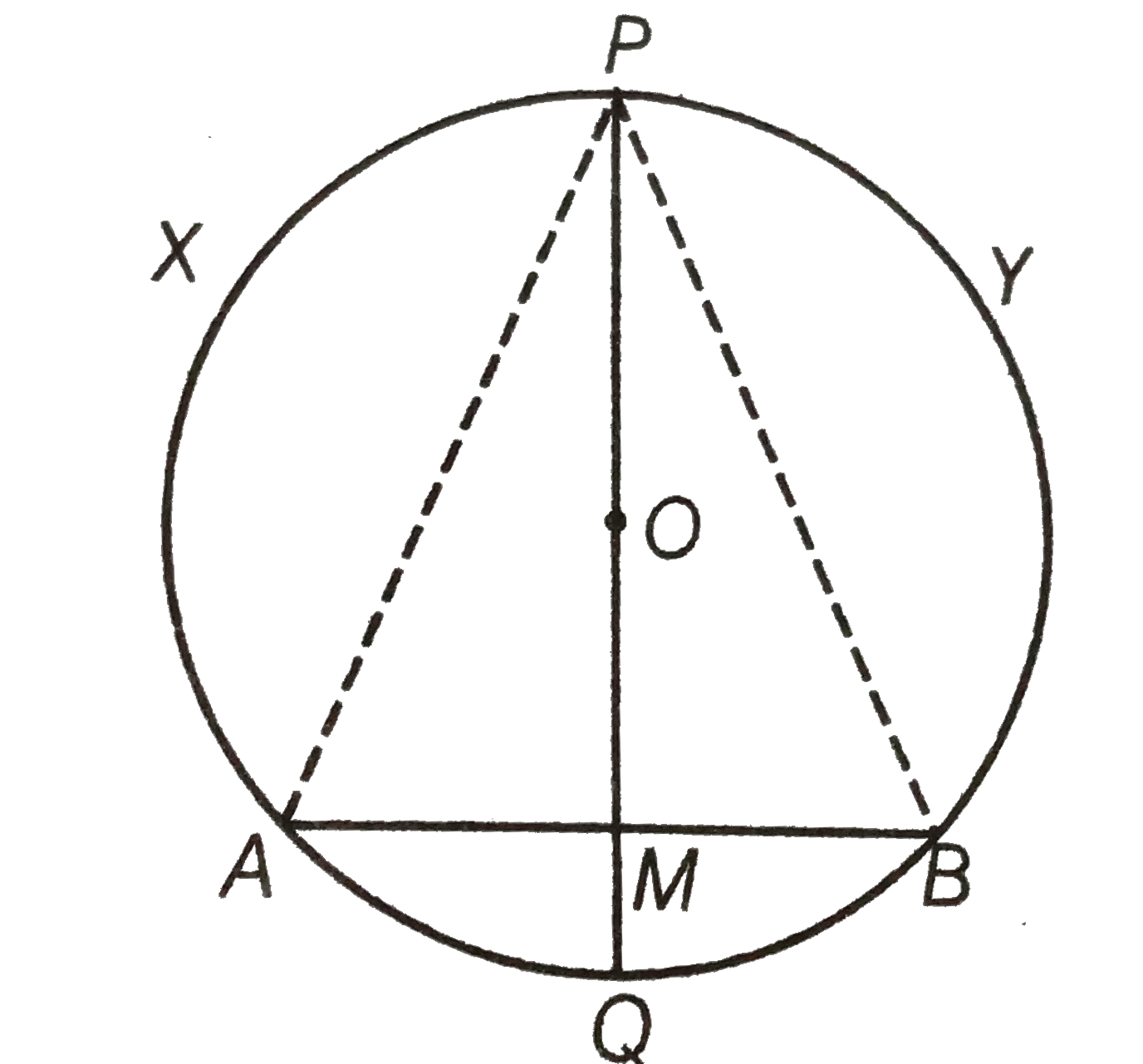
To prove arc `PXA cong "arc "PYB`
Construction Join AP and BP.
Proof in `Delta APM and DeltaBPM`,
AM=MB [`:'` PM bisects AB]
`anglePMA=anglePMB [:' PMbotAB]`
PM=PM [common side]
`:. Delta APM cong DeltaBPM ` [by SAS congruence rule]
`:.` PA=PB [by CPCT]
`rArr "arc "PXA cong "arc "PYB `
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    NCERT EXEMPLAR|Exercise Exercise 10.4|2 Videos

  • Areas of Parallelograms and Triangles

    NCERT EXEMPLAR|Exercise Areas Of Parallelograms And Triangles|34 Videos

  • CONSTRUCTIONS

    NCERT EXEMPLAR|Exercise Long Answer Type Questions|5 Videos

Similar Questions

Explore conceptually related problems

Arc of a Circle

Prove that the perpendicular bisector of a chord of a circle always passes through the centre.

Prove that the right bisector of a chord of a circle,bisects the corresponding arc or the circle.

Prove that the right bisector of a chord of a circle,bisects the corresponding arc or the circle.

In the figure, two circles touch internally at point P. chord AB of the larger circle intersects the smaller circle in C and D. Prove /_CPA cong /_DPB .

In the given figure, centre of two circles is O. Chord AB of bigger circle intersects the smaller circle in points P and Q . Show that AP = BQ.

In figure, chord AB cong chord CD, Prove that, arc AC cong arc BD.

The number of arcs made by a chord on a circle is___

In the adjoining figure , circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the other circle intersects innet circle at point A. Prove that, seg EA cong seg AB.