Home
Class 9
MATHS
A, B and C are three points on a circle....

`A`, `B` and `C` are three points on a circle. Prove that the perpendicular bisectors of `AB`, `BC` and `CA` are concurrent.

Text Solution

Verified by Experts


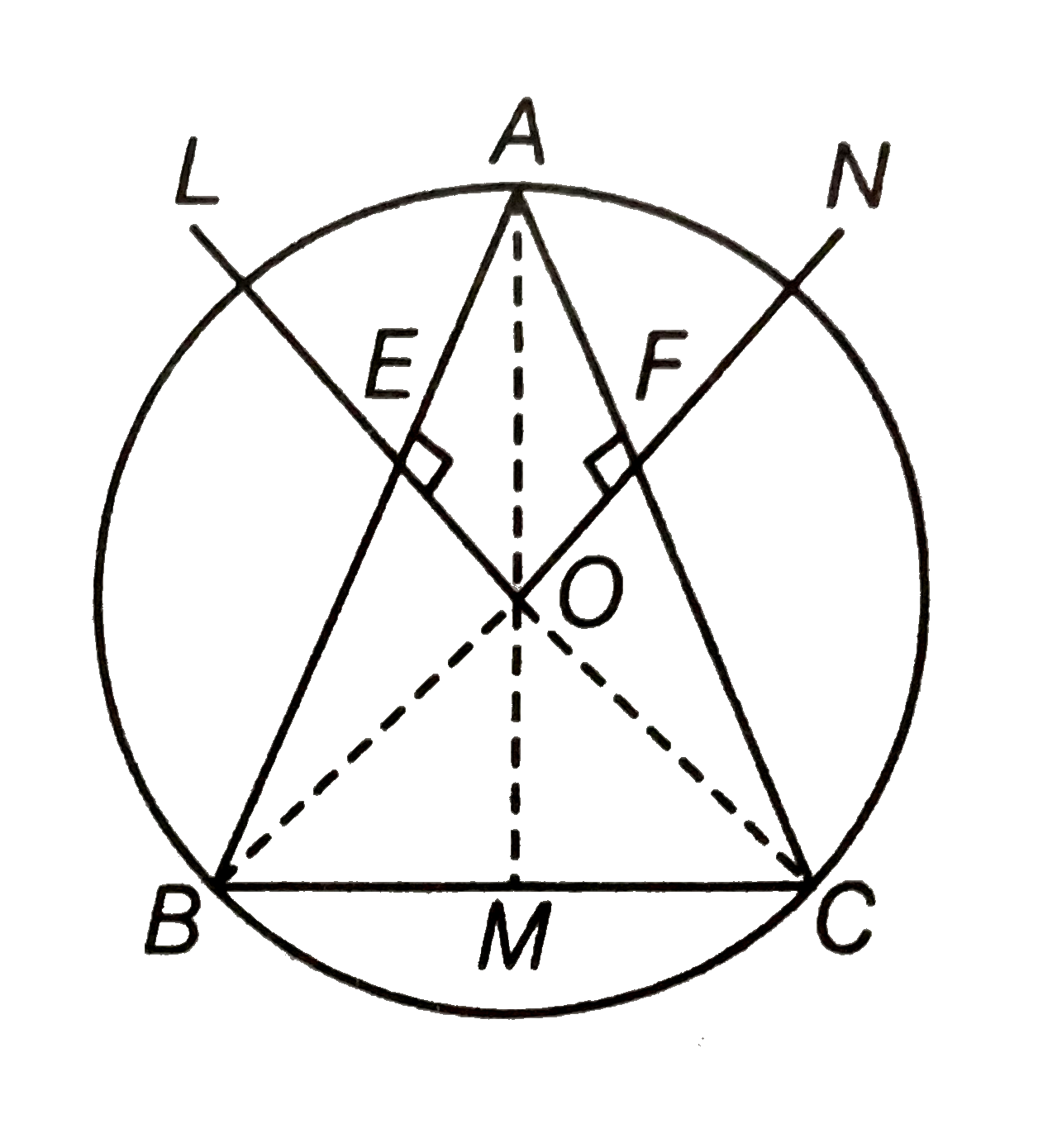
Given A circle passing through three points, A, B and C.
Construction Draw perpendicular bisectors of AB and AC and they meet at a point O. Join OA, OB and OC.
To prove Perpendicular bisector of BC, also passes through O i.e, LO,ON and OM are concurrent.
Proof In `DeltaOEA and DeltaOEB`,
AE=BE
[OL is the perpendicular bisector of AB]
`angleAEO=angleBEO ["each "90^(@)]`
and OE=OE [common side]
`:. Delta OEA cong OEB` [by SAS congruence rule]
`:. OA=OB`
Similarly, `DeltaOFA cong DeltaOFC` [by SAS congruence rule]
`:. OA=OC` [by CPCT]
`:. OA=OB=OC=r` [say]
Now, we draw a perpendicular from O to the BC and join them.
In `DeltaOMB and DeltaOMC`,
OB=OC [proved above]
OM=OM [common side]
and `angleOMB = angleOMC ["each "90^(@)]`
` :. DeltaOMB cong DeltaOMC` [by RHS congruence rule]
`rArr BM=MC` [by CPCT]
Hence, OM is the perpendicular bisector of BC.
Hence, OL, ON and OM are concurrent.
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    NCERT EXEMPLAR|Exercise Exercise 10.4|2 Videos

  • Areas of Parallelograms and Triangles

    NCERT EXEMPLAR|Exercise Areas Of Parallelograms And Triangles|34 Videos

  • CONSTRUCTIONS

    NCERT EXEMPLAR|Exercise Long Answer Type Questions|5 Videos

Similar Questions

Explore conceptually related problems

Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.

From a point O inside a triangle ABC , perpendiculars OD,OE and Of are drawn to rthe sides BC,CA and AB, respecrtively. Prove that the perpendiculars from A,B, and C to the sides EF, FD and DE are concurrent.

From a point O inside a triangle ABC, perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB, respectively. Prove that the perpendiculars from A, B and C to the sides EF, FD and DE are concurrent

In Figure,widehat AB~=widehat AC and O is the centre of the circle.Prove that OA is the perpendicular bisector of BC

If A.B and C are three points on a line,and B lies between A and C then prove that AB-BC=AC

If A, B and C are three points on a line and B is between A and C then prove that AC - BC = AB.

From an external point P, two tangents PAandPB are drawn to the circle with centre O .Prove that OP is the perpendicular bisector of AB.

Let ABC and PQR be any two triangles in the same plane. Assume that the perpendiculars from the points A, B, C to the sides QR, RP, PQ respectively are concurrent. Using vector methods or otherwise,prove that the perpendiculars from P, Q, R to BC, CA, AB respectively are also concurrent.

If A, B and C are three points on a line, and B lies between A and C (see figure), then prove that AB + BC = AC.