Home
Class 9
MATHS
Two chords A B and A C of a circle are e...

Two chords `A B` and `A C` of a circle are equal. Prove that the centre of the circle lies on the angle bisector of `/_B A Cdot`

Text Solution

Verified by Experts

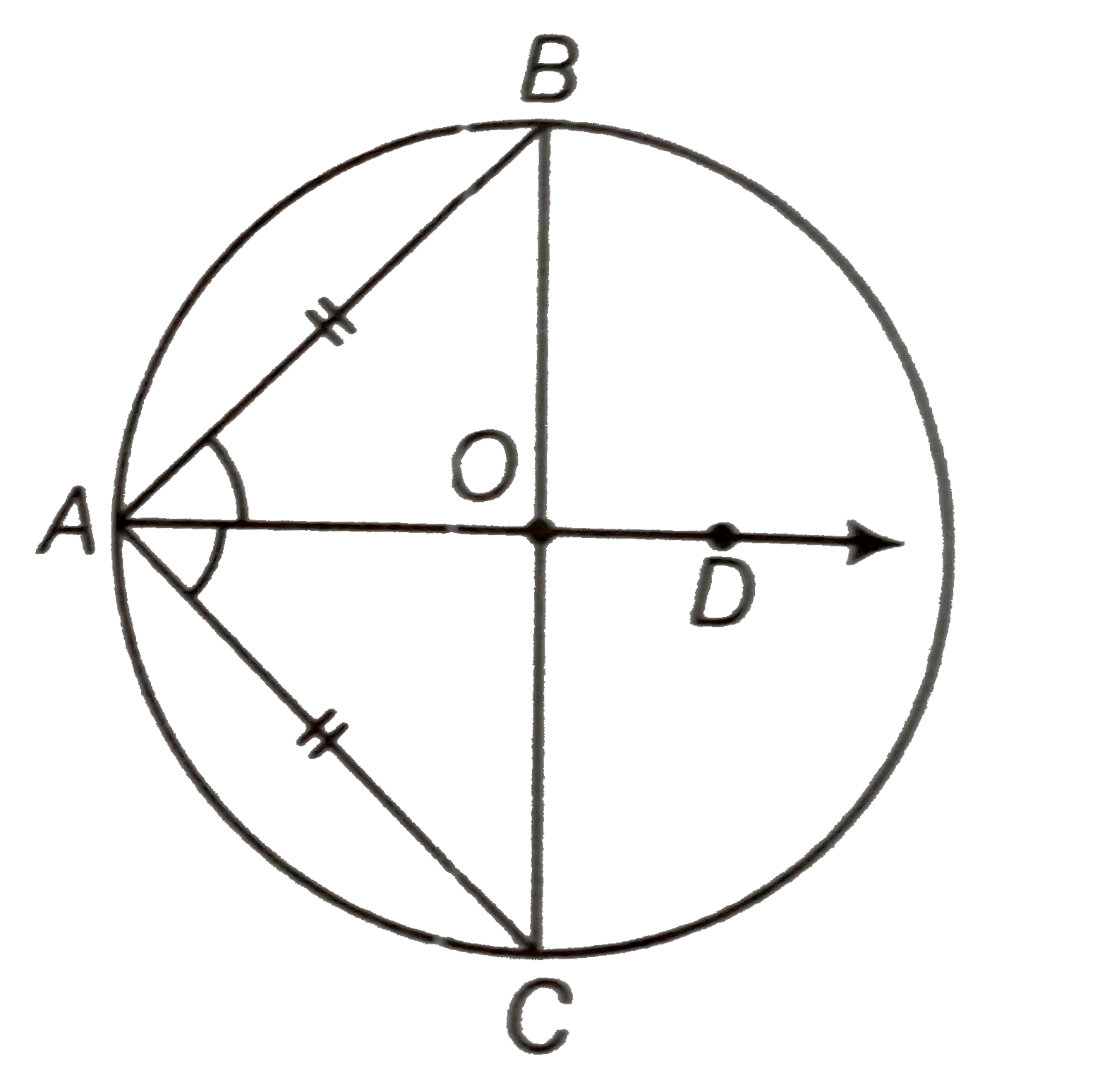
Given AB and AC are two equal chords whose centre is O.
To prove Centre O lies on the bisector of `angleBAC`.
Construction Join BC, draw bisector AD of `angleBAC`.
Proof In `DeltaBAM and DeltaCAM`,
AB=AC [given]
`angleBAM=angleCAM ` [given]
and AM=AM [common side]
`:. DeltaBAM cong DeltaCAM` [by SAS congruence rule]
`rArr BM=CM` [by CPCT]
and `angleBMA=angleCMA` [by CPCT]
So, `BM=CM and angleBMA=angleCMA=90^(@)`
So, AM is the perpendicular bisector of the chord BC.
Hence, bisector of `angleBAC` i.e., AM passes through the centre O.
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    NCERT EXEMPLAR|Exercise Exercise 10.4|2 Videos

  • Areas of Parallelograms and Triangles

    NCERT EXEMPLAR|Exercise Areas Of Parallelograms And Triangles|34 Videos

  • CONSTRUCTIONS

    NCERT EXEMPLAR|Exercise Long Answer Type Questions|5 Videos

Similar Questions

Explore conceptually related problems

Two chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of /_BAC.

Two chord AB and AC of a circle are equal. Prove that the centre of a circle lies on the angle bisector of /_BAC

If two chords AB and AB of a circle with centre O are such that the centre O lies on the bisector of /_BAC; Prove that AB=AC

If two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of /_BAC, prove that AB=AC, i.e. the chords are equal.

Equal chords of a circle are equidistant from the centre.

Equal chords of a circle subtend equal angles at the centre.

Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.

Theorem 10.1 : Equal chords of a circle subtend equal angles at the centre

Theorem: 4( iii) If two equal chords are drawn from a point on the circle; then the centre of a circle will lie on angle bisector of these two chords.

If the length of a chord of a circle is equal to that of the radius of the circle , then the angle subtended , in radians , at the centre of the circle by the chord is