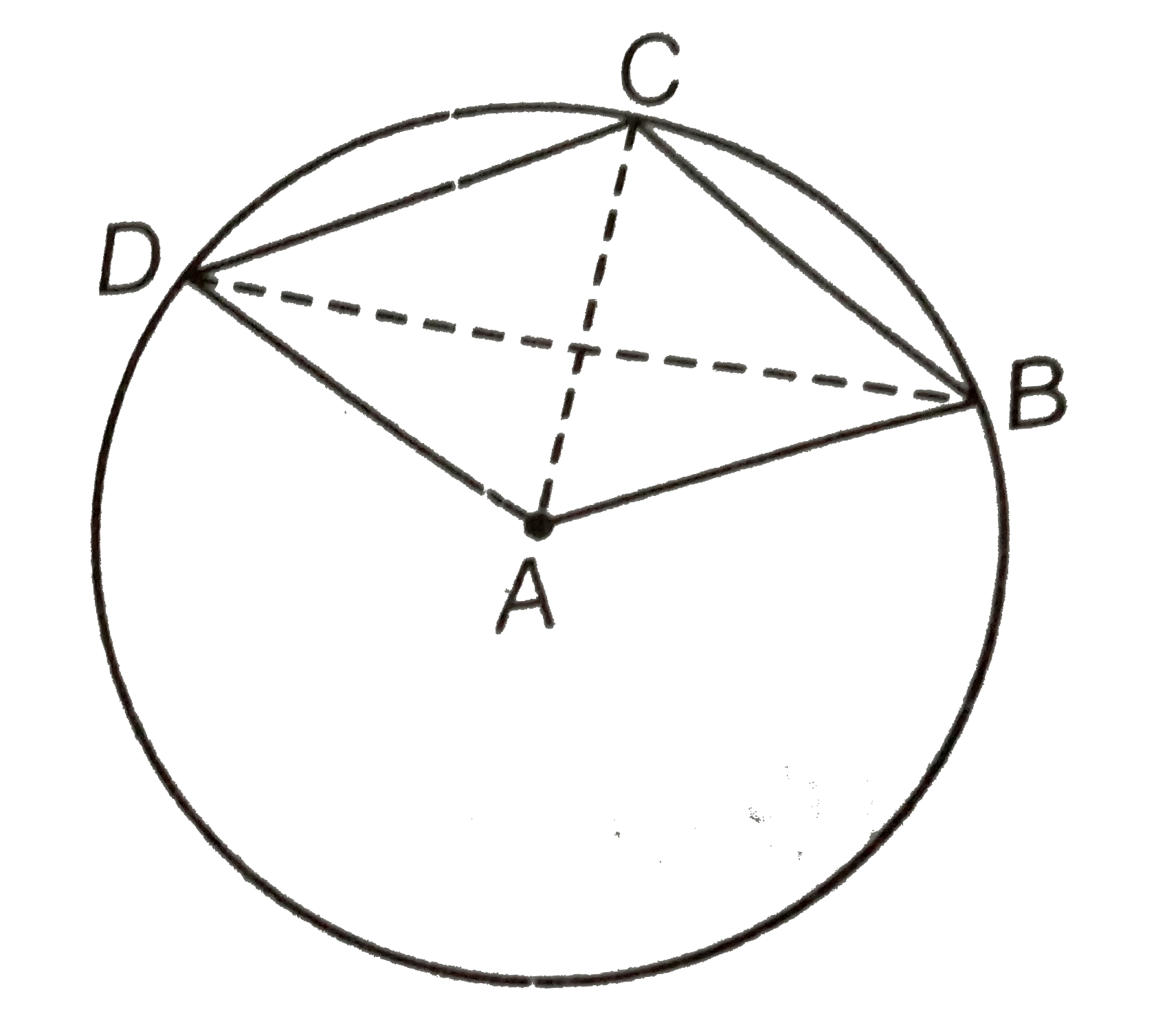
Given In a circle, ABCD is a wuadrilateral having centre A.
To prove `angleCBD+angleCDB=1/2angleBAD`
Construction Join AC and BD.
Proof Since, arc DC subtends `angleDAC` at the centre and `angleCBD` at a point B in the remaining part of the circle.
`:. angleDAC=2angleCBD ...(i)`
In a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
Similarly, arc BC subtends `angleCAB` at the centre and `angleCDB` at a point D in the remaining part of the circle.
`:. angleCAB=2angleCDB ....(ii)`
In a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
On adding Eqs. (i) and (ii), we get
`angleDAC+angleCAB=2angleCBD+2angleCDB`
`rArr angleBAD=2(angleCBD+angleCDB)`
`rArr angleCDB+angleCBD=1/2angleBAD`