Home
Class 9
MATHS
If O is the circumcentre of a A B C and...

If `O` is the circumcentre of a ` A B C` and `O D_|_B C ,` prove that `/_B O D=/_adot`

Text Solution

Verified by Experts

Given In a `DeltaABC` a circle is circumscribed having centreO.

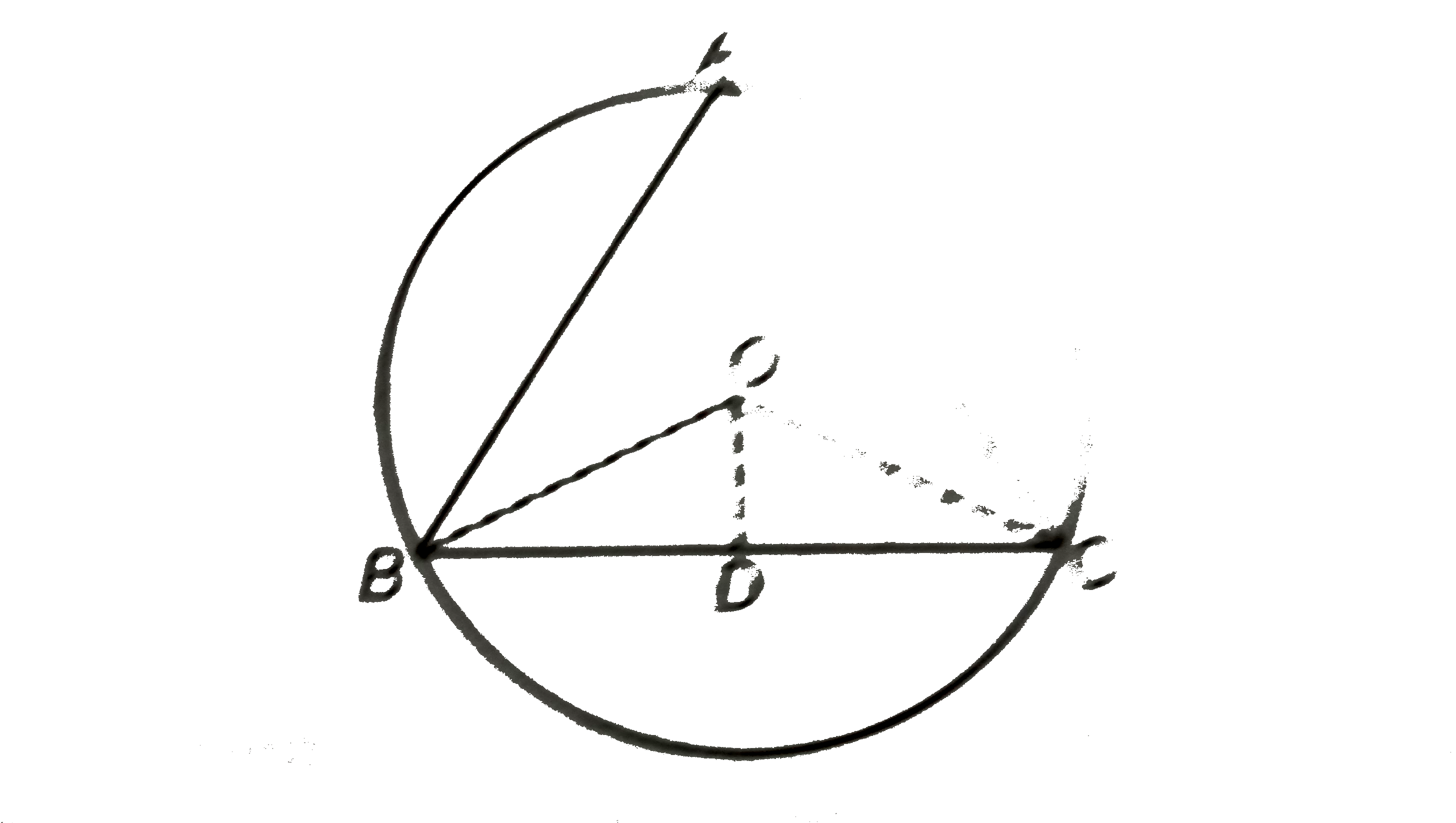
Also, D is the mid-point of BC.
To prove `angleBOD=angleA or angleBOD=angleBAC`
Construction Join OB, OD and OC.
Proof In `DeltaBOD and DeltaCOD`,
OB=OC [both are the radius of circle]
BD=DC [D is the mid-point of BC]
and OD=OD [common side]
`:. Delta BOD cong DeltaCOD` [by SSS congruence rule]
`:. angleBOD=angleCOD` [by CPCT]...(i)
We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
`:. 2angleBAC=angleBOC`
`rArr angleBAC=2/2angleBOD [:' angleBOC=2 angleBOD]` [from Eq. (i)]
`rArr angle BAC=angleBOD`
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    NCERT EXEMPLAR|Exercise Exercise 10.4|2 Videos

  • Areas of Parallelograms and Triangles

    NCERT EXEMPLAR|Exercise Areas Of Parallelograms And Triangles|34 Videos

  • CONSTRUCTIONS

    NCERT EXEMPLAR|Exercise Long Answer Type Questions|5 Videos

Similar Questions

Explore conceptually related problems

If ' O ' is the circum centre of the A B C and R_1,\ R_2,\ R_3 are the radii of the circumcircle of triangle O B C ,\ O C A\ a n d\ O A B respectively then a/(R_1)+b/(R_2)+c/(R_3) has the value equal to (a b c)/(2R^3) (b) (R^3)/(a b c) (c) (4)/(R^2) (d) (a b c)/(R^3)

Bisector A D of /_B A C of A B C passes through the centre O of the circumcircle of A B C as shown in figure. Prove that A B=A Cdot

In figure, O is a point in the interior of a triangle ABC, O D_|_B C ,O E_|_A C and O F_|_A B . Show that (i) O A^2+O B^2+O C^2-O D^2-O E^2-O F^2=A F^2+B D^2+C E^2 (ii) A F^2+B D^2+C E^2=A W^2+C D^2+B F^2

D is the mid-point of side B C of A B C and E is the mid-point of B Ddot If O is the mid-point of A E , prove that a r( B O E)=1/8a r( A B C)

D is the mid-point of side B C of \ A B C\ a n d\ E is the mid-point of B Ddot If O is the mid-point of A E , prove that a r\ (\ B O E)=1/8a r\ (\ A B C)

If O\ a n d\ O^(prime) are circumcentre and orthocentre of \ A B C ,\ t h e n\ vec O A+ vec O B+ vec O C equals a. 2 vec O O ' b. vec O O ' c. vec O ' O d. 2 vec O ' O

Diagonals A C and B D of a quadrilateral A B C D intersect at O in such a way that a r( A O D)=a r( B O C) . Prove that A B C D is a trapezium.

In figure, ABC is triangle in which /_A B C > 90o and A D_|_C B produced. Prove that A C^2=A B^2+B C^2+2B C.B D .

A B C D is a parallelogram whose diagonals A C and B D intersect at Odot A Line through O intersects A B at P and D C at Qdot Prove that a r( P O A)=a r( Q O C)dot

In fig., O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:- O A^ 2 + O B^ 2 + O C^ 2 − O D^ 2 − O E^ 2 − O F^ 2 = A F^ 2 + B D^ 2 + C E^ 2