Home
Class 9
MATHS
On a common hypotenuse AB, two right ang...

On a common hypotenuse AB, two right angled triangles, ACB and ADB are situated on opposite sides. Prove that `angleBAC=angleBDC`.

Text Solution

Verified by Experts

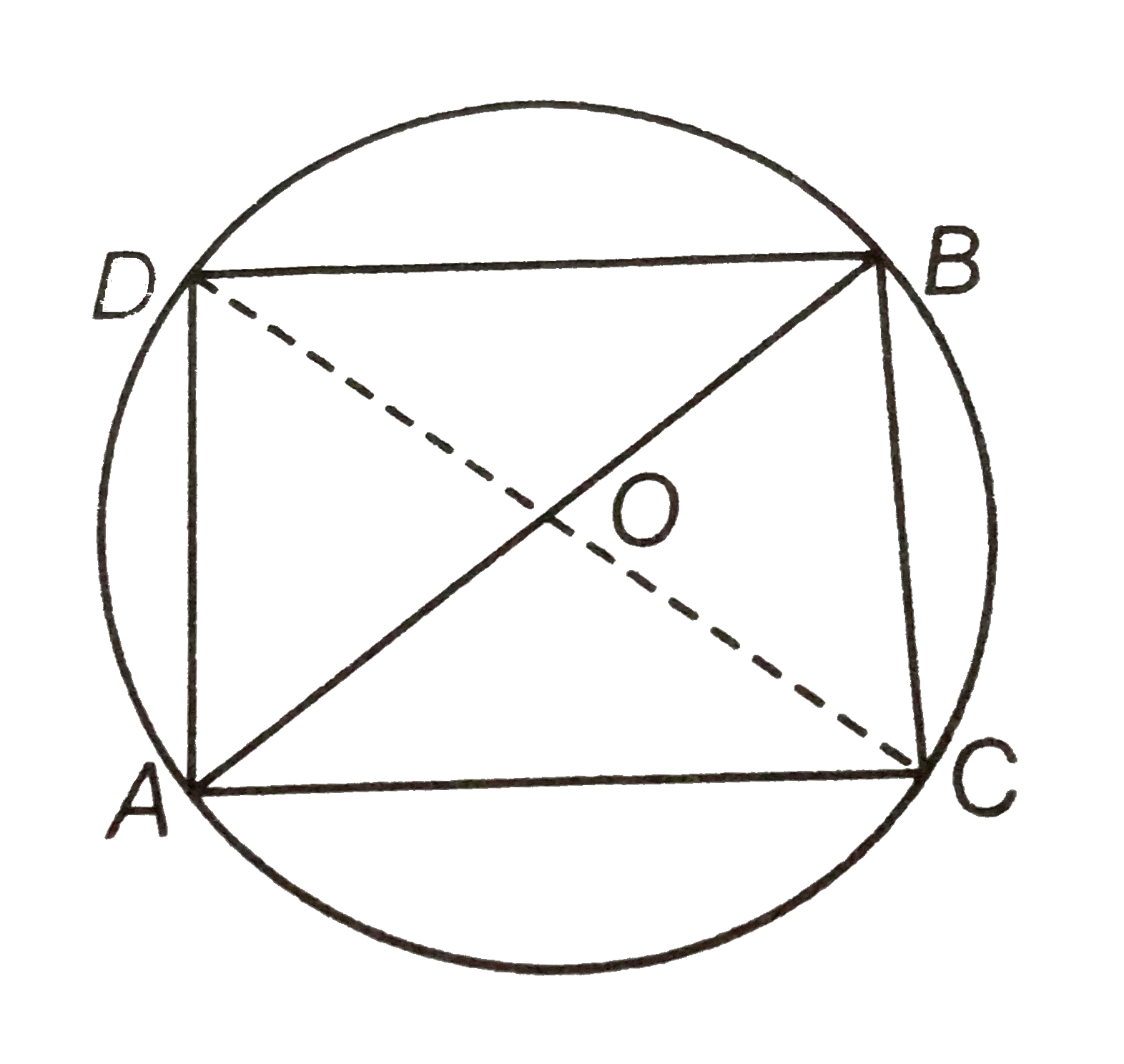
Given, `DeltaACB and Delta ADB` are two right angled triangles with common hypotenuse AB.
To prove `angleBAC=angleBDC`
Construction join CD.
Proof Let O be the mid-point of AB.
Then, OA=OB =OC=OD.
Since, mid-point of the hypotenuse of a right triangle is equidistant from its vertices. Now, draw a circle to pass through the points A, B, C and D. with O as centre and radius equal to OA.
We know that, angles in the same segment of a circle are equal. From the figure, `angleBAC and angleBDC` are angles of same segment BC.
`:. angleBAC= angleBDC`
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    NCERT EXEMPLAR|Exercise Exercise 10.4|2 Videos

  • Areas of Parallelograms and Triangles

    NCERT EXEMPLAR|Exercise Areas Of Parallelograms And Triangles|34 Videos

  • CONSTRUCTIONS

    NCERT EXEMPLAR|Exercise Long Answer Type Questions|5 Videos

Similar Questions

Explore conceptually related problems

Show that in a right angled triangle,the hypotenuse is the longest side.

Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.

A side of an isosceles right angled triangle is x. Find its hypotenuse.

A right angled triangle has legs 1 and x . The hypotenuse is y and angle opposite to the side x is theta . Shown as

A point D is taken from the side BC of a right angled triangle ABC, where AB is hypotenuse. Then,

Find the length of the hypotenuse in a right angled triangle where the sum of the squares of the sides making right angle is 169.

In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab=cx