Home
Class 9
MATHS
Two chords AB and AC of a circle subtend...

Two chords AB and AC of a circle subtends angles equal to `90^(@) and 150^(@)`, respectively at the centre. Find`angleBAC`, if AB and AC lie on the opposite sides of the centre.

Text Solution

Verified by Experts

In `DeltaBOA, OB=OA` [both are the radius of circle]
`:. angleOAB=angleOBA …(i)`
[angles opposite to equal sides are equal]

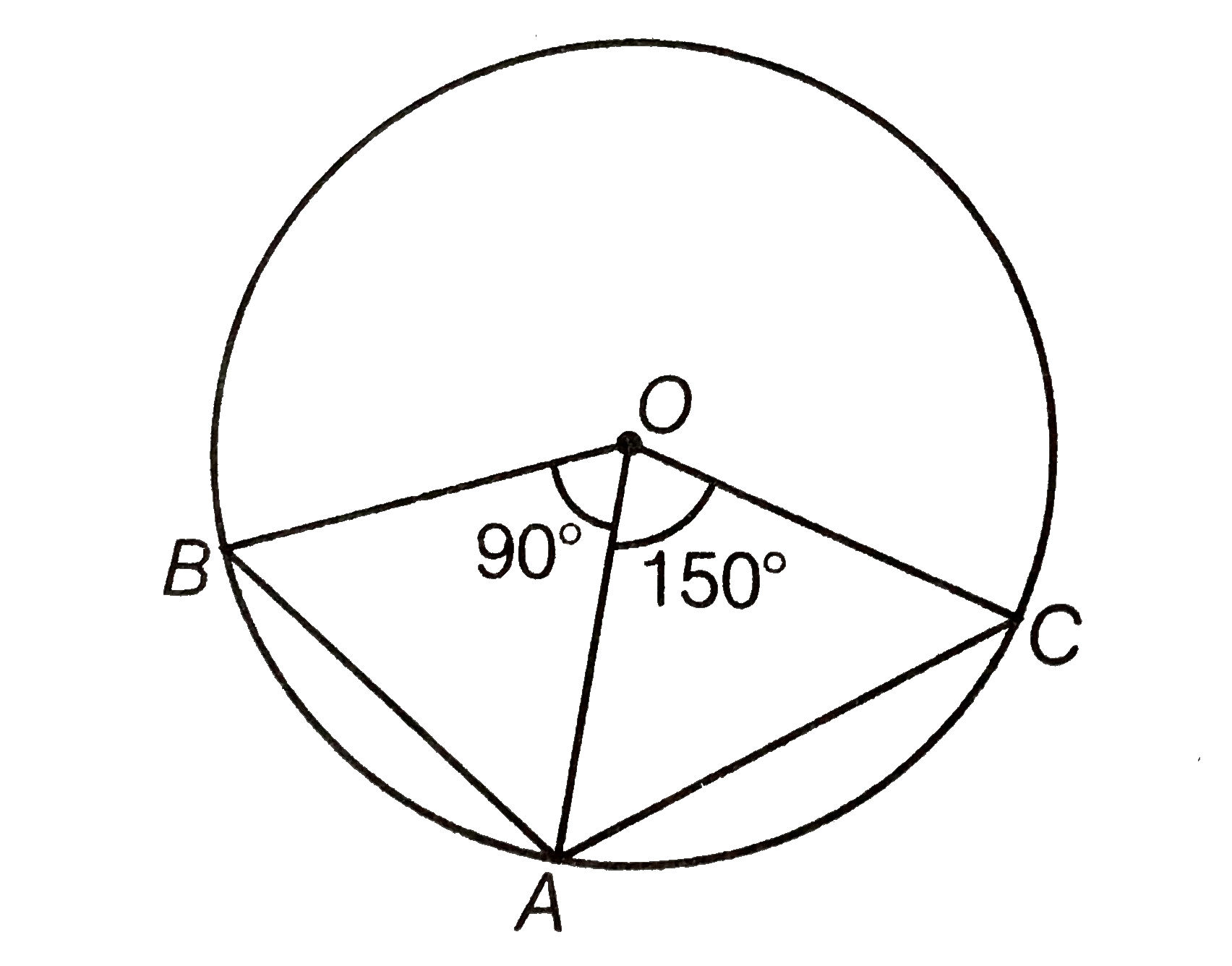
In `DeltaOAB, angleOBA+angleOAB+angleAOB=180^(@)` [by angle sum property of a triangle]
`rArr angleOAB+angleOAB+90^(@)=180^(@)` [from Eq. (i)]
`rArr 2angleOAB=180^(@)-90^(@)`
`rArr angleOAB=90^(@)/2=45^(@)`
Now, in `DeltaAOC, AO=OC` [both are the redius of a circle]
`:. angleOCA=angleOAC`...(ii)
[angles opposite to equal sides are equal]
Also, `angleAOC+angleOAC+angleOCA=180^(@)` [by angle sum property of a triangle]
`rArr 150^(@)+2 angleOAC=180^(@)` [from Eq. (ii)]
`rArr 2angleOAC=180^(@)-150^(@)`
`rArr 2 angle OAC=30^(@)`
`rArr angleOAC=15^(@)`
`:. angleBAC=angleOAB+angleOAC=45^(@)+15^(@)=60^(@)`
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    NCERT EXEMPLAR|Exercise Exercise 10.4|2 Videos

  • Areas of Parallelograms and Triangles

    NCERT EXEMPLAR|Exercise Areas Of Parallelograms And Triangles|34 Videos

  • CONSTRUCTIONS

    NCERT EXEMPLAR|Exercise Long Answer Type Questions|5 Videos

Similar Questions

Explore conceptually related problems

Equal chords of a circle subtend equal angles at the centre.

Equal chord of circle subtends equal angle on centre.

Let p and q be the length of two chords of a circle which subtend angles 36^@ and 60^@ respectively at the centre of the circle . Then , the angle (in radian) subtended by the chord of length p + q at the centre of the circle is (use pi=3.1 )

Prove that equal chords of a circle subtend equal angles at the centre.

Theorem 10.1 : Equal chords of a circle subtend equal angles at the centre

Equal chords of congruent circles subtend equal angles at the centre.

Equal chords of congruent circles subtend equal angles at the centre.

Two chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of /_BAC.

In a circle of radius 5 cm, AB and CD are two parallel chords of lengths 8 cm and 6 cm respectively. Calculate the distance between the chords if they are (i) on the same side of the centre. (ii) on the opposite sides of the centre.

Two chord AB and AC of a circle are equal. Prove that the centre of a circle lies on the angle bisector of /_BAC