If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral, so formed is cyclic.

Explanation

Given `DeltaABC` is an isosceles triangle such that AB=AC and also `DE||BC`.
To prove Quadrilateral BCDE is a cyclic quadrilateral.
Construction Draw a circle passes through the points B, C, D and E.

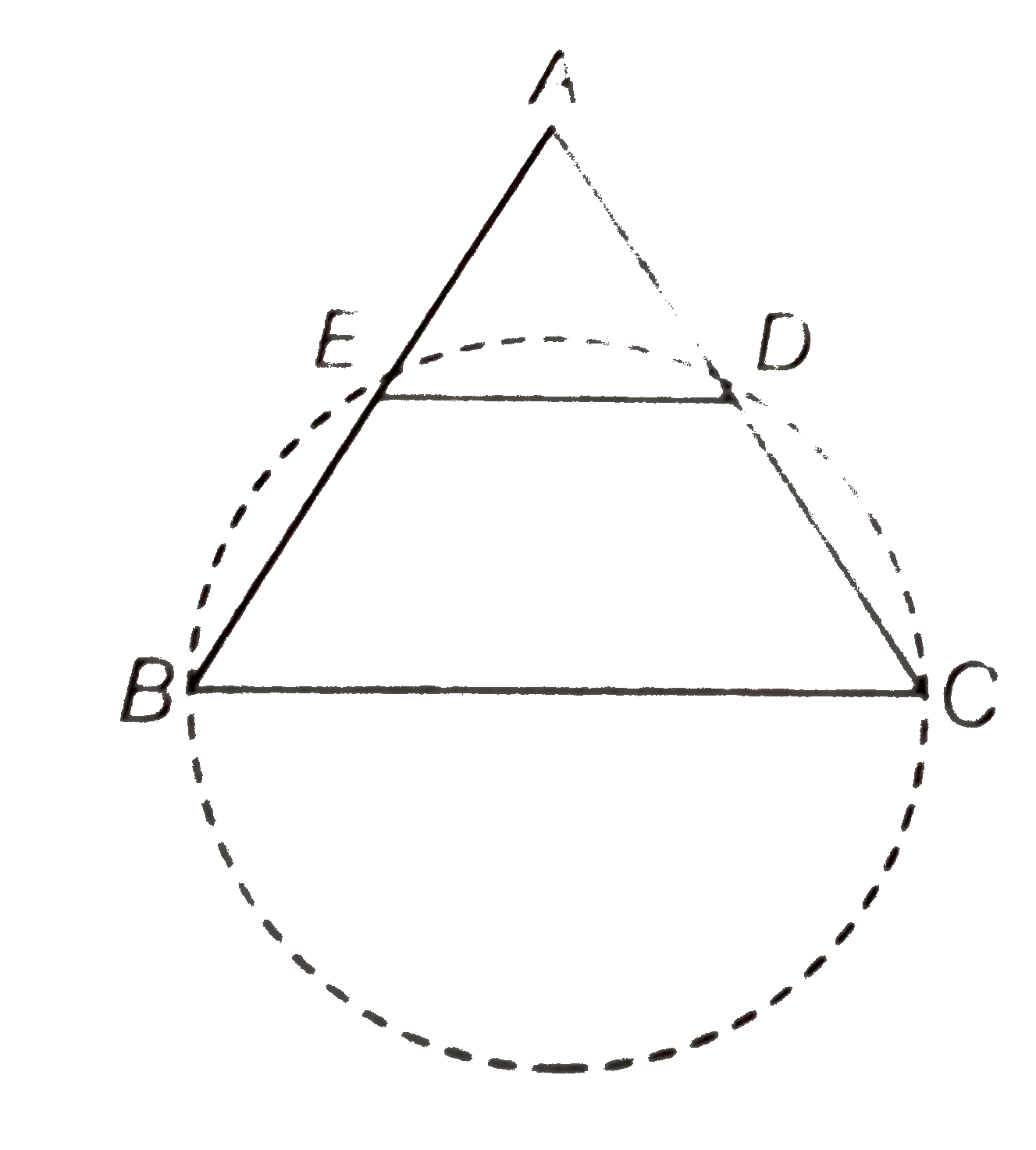
Proof In `DeltaABC, AB=AC` [equal sides of an isosceles triangle]
`rArr angleACB=angleABC ...(i)`
[angle opposite to the equal sides are equal]
Since, `DE||BC`
`rArr angleADE=angleACB` [corresponding angles]...(ii)
On adding both sides by `angleEDC ` in Eq. (ii), we get
`angleADE+angleEDC=angleACB+angleEDC`
`rArr 180^(@)=angleACB+angleEDC`
[`angleADE and angleEDC` form linear pair aniom]
`rArr angleEDC+angleABC=180^(@)` [form Eq. (i)]
Hence, BCDE is a cyclic quadrilateral, because sum of the opposite angles is `180^(@)`.