Given A circle is circumscribed on a ` DeltaABC` having centre O.
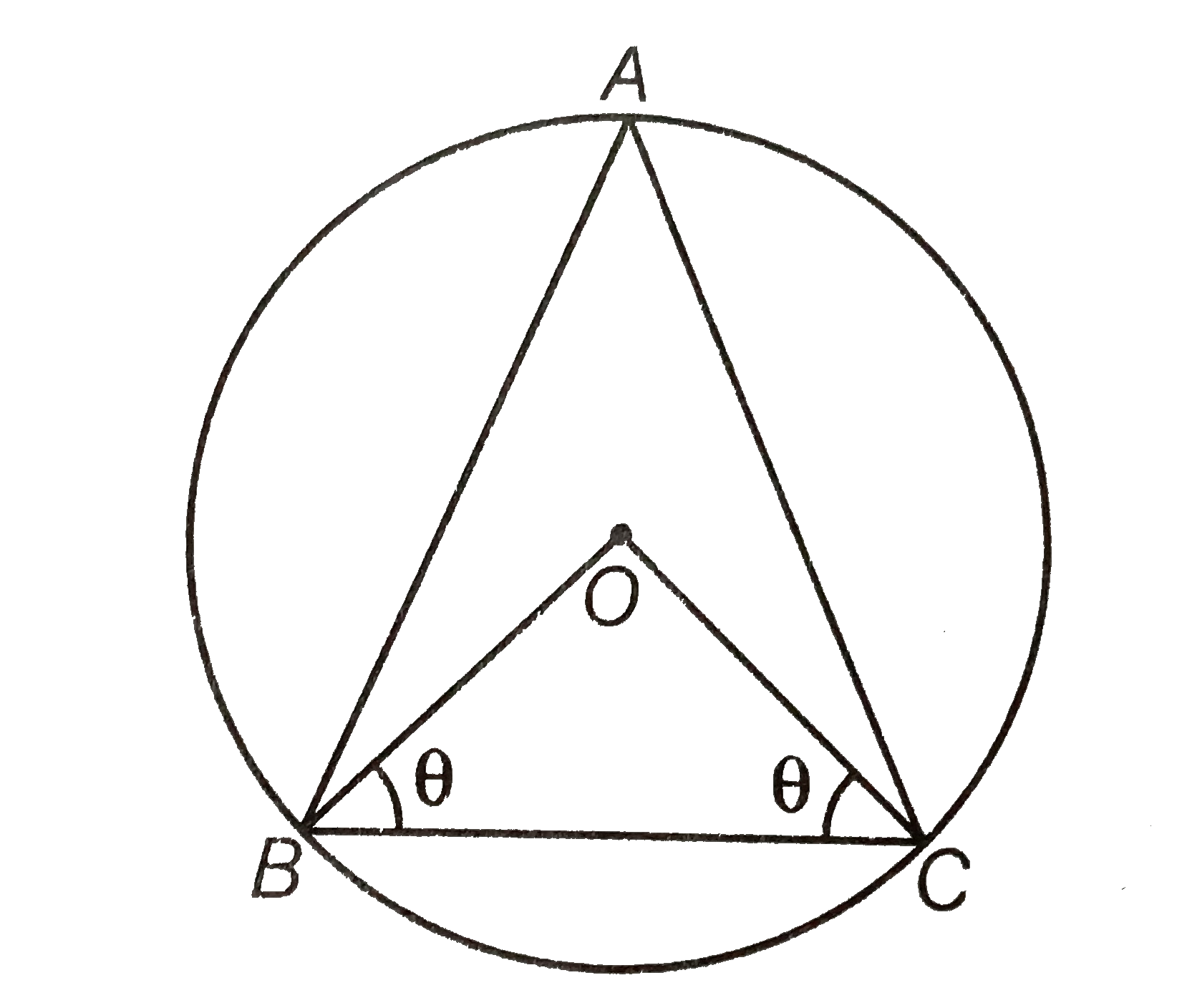
To prove `angleOBC+angleBAC=90^(@)`
Construction Join BO and CO.
Proof Let ` angleOBC=angleOCB=theta`…(i)
In ` DeltaOBC, angleBOC+angleOCB+angleCBO=180^(@)`
[by angle sum property of a triangle is `180^(@)`]
`rArr angleBOC+theta+theta=180^(@)`
`rArr angleBOC=180^(@)-2theta`
We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
`:. angleBOC=2angleBAC`
`rArr angleBAC=(angleBOC)/2=(180^(@)-2theta)/2=90^(@)-theta`
`rArr angleBAC+theta=90^(@) `
`:. angleBAC+angleOBC=90^(@)` [from Eq. (i)]