In Figure, `A B C D` is a cyclic quadrilateral whose side `A B` is a diameter of the circle through `A ,\ B ,\ C ,\ Ddot` If `(/_A D C)=130^0,`find `/_B A C`

Explanation

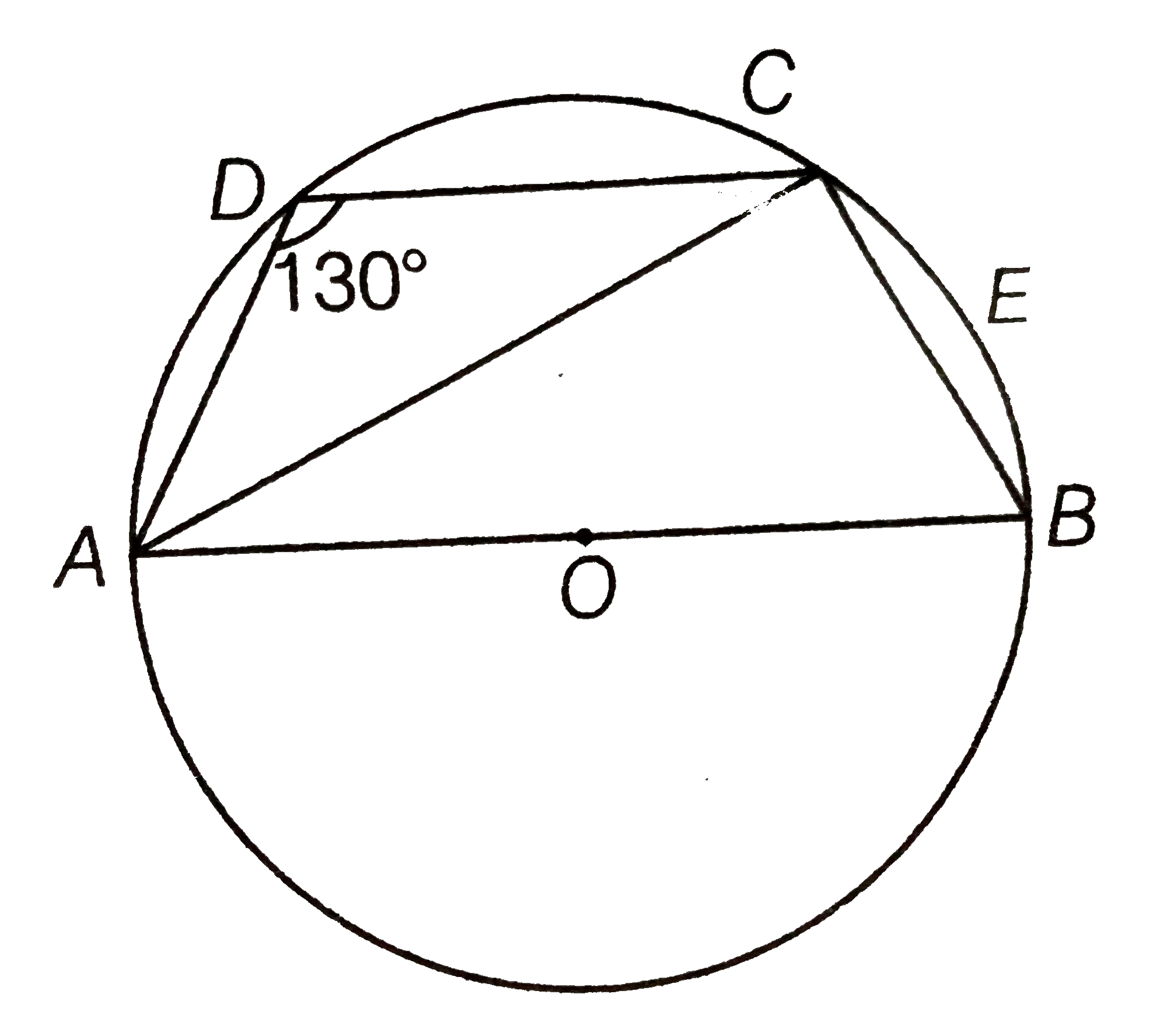
Draw a quadrilateral ABCD inscribed in a circle having centre O. Given, `angleADC=130^(@)`
Since, ABCD is a quadrilateral inscribed in a circle, therefore ABCD becomes a cyclic quadrilateral.
`:'" Since, the sum of opposite angles of a cyclic quadrilateral is "180^(@)`.
`:. angleADC+angleABC=180^(@)`
`rArr 130^(@)+angleABC=180^(@)`
`rArr angleABC=50^(@)`
Since, AB is a diameter of a circle, then AB subtends an angle to the circle is right angle.
`:. angleACB=90^(@)`
In `DeltaABC, angleBAC+angleACB+angleABC=180^(@)` [by angle sum property of a triangle]
`rArr angleBAC+90^(@)+50^(@)=180^(@)`
`rArr angleBAC=180^(@)-(90^(@)+50^(@))`
`=180^(@)-140^(@)=40^(@)`